Modellierung

Leiten Sie für beide unten abgebildeten Masse- Feder-Dämpfer Systeme ein mathematisches Modell her und bestimmen Sie die Ruhelage des Systems. Gehen Sie dazu jeweils wie folgt vor:

1. Identifizieren Sie die Energiespeicher ('reservoirs') und die zugehörigen Speichergrößen ('level variables').
2. Identifizieren Sie Zu- und Abflüsse ('flows'). Überlegen Sie sich dazu welche Masseinheit diese Flüsse haben müssen.
3. Formulieren Sie die Energiebilanzgleichungen für System A und B
4. Bestimmen sie die Ruhelage des Systems aus den gewonnenen Differentialgleichungen.

Bemerkungen: Es wirke zusätzlich zur Erdbeschleunigung jeweils die externe Kraft auf die Masse . Die Länge der entspannten Feder beträgt

Gegeben ist der dargestellte Tankbehälter.

Es sind folgende linearisierte Differentialgleichungen in der Ruhelage des Systems bei einem konstanten Zufluss bekannt. 

a) Geben Sie eine Differentialgleichung an, die den Füllstand in Abhängigkeit vom Zufluss beschreibt.
b) Transformieren Sie beide gegebenen Differentialgleichungen in den Laplace-Bereich. Geben Sie einen Ausdruck für den Füllstand in Abhängigkeit des Zuflusses an.

Hinweis: Im folgenden gilt:

c) Bestimmen Sie den zeitlichen Verlauf des Füllstandes der aus den gegebenen Anfangswerten für und resultiert. Es wird angenommen, dass keine zusätzliche Flüssigkeit in den Tank A fließt

Eine Brennstoffzelle ist eine elektrochemische Zelle, die die Reaktionsenergie eines kontinuierlich zugeführten Brennstoffes (z.B. Wasserstoff) und eines Oxidationsmittels (z.B. Sauerstoff bzw. Luft) in nutzbare elektrische Energie umwandelt. Bei dieser Reaktion entsteht neben Wasser als Reaktionsprodukt immer auch Wärme. Um ein Überhitzen der Brennstoffzelle zu vermeiden, muss die Reaktionswärme laufend abgeführt werden.

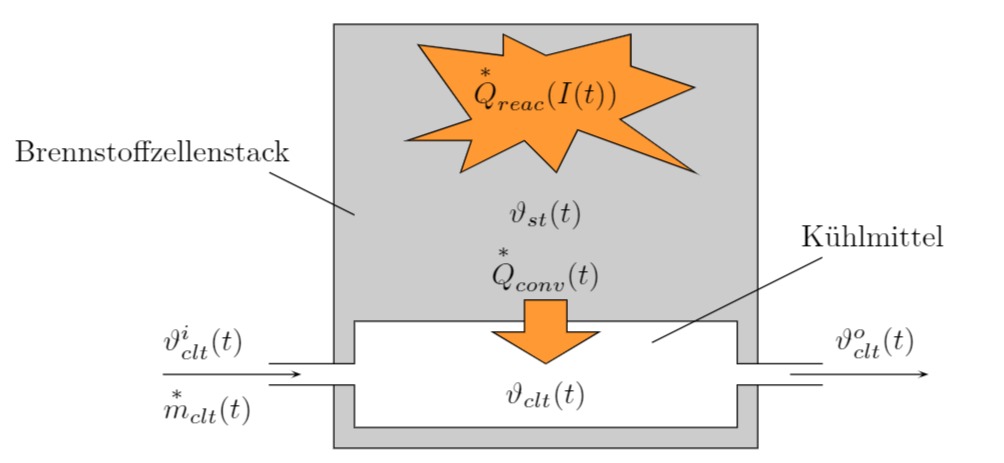
In dieser Aufgabe soll für einen wassergekühlten Brennstoffzellenstack (Serienschaltung mehrerer einzelner Brennstoffzellen) ein thermisches Modell erstellt und analysiert werden. Dazu werden die folgenden vereinfachenden Annahmen gemacht:

• Reduktion auf zwei thermische Speicher (Brennstoffzellenstack, Kühlmittel)
• Homogene Temperaturverteilung in den Speichern
• Kein Wärmeverlust über die Oberfläche des Stacks an die Umgebung
• Temperaturunabhängige Systemparameter

Weiter ist folgende Gleichung für die Reaktionswärme gegeben,

und angenommen, dass zwischen Stack und Kühlmittel ein konvektiver Wärmetransfer stattfindet,

Die Kühlmittelaustrittstemperatur soll gleich der Kühlmitteltemperatur gesetzt werden «perfect mixing"»,

Aufgabenstellungen

1. Stellen Sie die Energiebilanzen (1. Hauptsatz) für die beiden thermischen Speicher auf und schreiben Sie das resultierende Differentialgleichungssystem 2. Ordnung an, mit:
   
2. Berechnen Sie die Gleichgewichtswerte und analytisch in Abhängigkeit der Betriebspunktwerte .
3. Linearisieren Sie das System um den Gleichgewichtspunkt und geben Sie die resultierenden Matrizen und an.
   
   Das konkrete System weise die folgenden Parameter- und Betriebspunktwerte auf:
   
4. Werten Sie die Systemmatrizen und numerisch aus.
5. Beurteilen Sie die Lyapunov-Stabilität des Systems.
6. Ist das System vollständig steuerbar?
7. Ist das System für und vollständig beobachtbar?
8. Berechnen Sie die Übertragungsmatrix des linearisierten Systems vom Eingang auf den Ausgang .
9. Welches Übertragungsverhalten wird durch den Eintrag der Übertragungsmatrix beschrieben? Geben Sie eine physikalische Interpretation der Ordnung und des statischen Übertragungsfaktors von .