Aufgabenstellung:
Gegeben ist der dargestellte Tankbehälter.
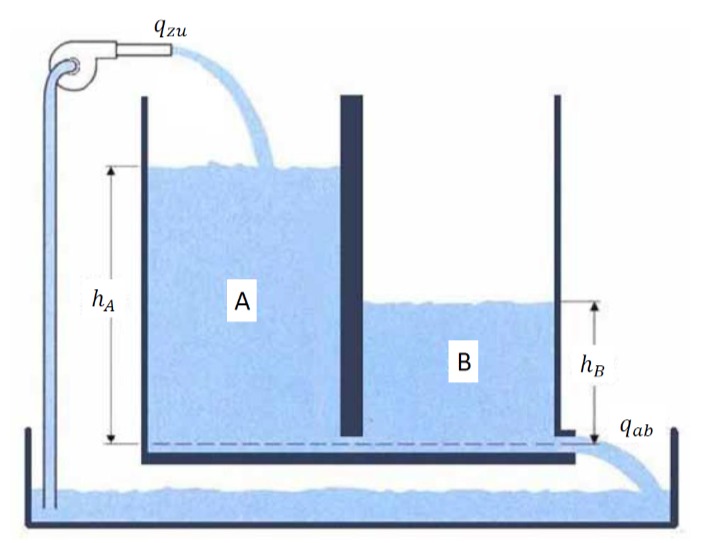
Es sind folgende linearisierte Differentialgleichungen in der Ruhelage des Systems bei einem konstanten Zufluss
a) Geben Sie eine Differentialgleichung an, die den Füllstand
b) Transformieren Sie beide gegebenen Differentialgleichungen in den Laplace-Bereich. Geben Sie einen Ausdruck für den Füllstand
Hinweis: Im folgenden gilt:
c) Bestimmen Sie den zeitlichen Verlauf des Füllstandes
Lösungsweg:
a) Differentialgleichungen
Es gilt die beiden Differentialgleichungen zu kombinieren, sodass die direkte Wirkung des Eingangs auf den Füllstand des Tanks B beschrieben wird.
Anmerkung: Es werden die linearisierten Differentialgleichungen des Problems betrachtet, sprich es wird ein System mit einem konstanten Zufluss und Abfluss betrachtet, welches eingeschwungen ist (keine Dynamik mehr vorhanden). Die betrachteten Gleichungen beschreiben nur die Abweichungen von diesem eingeschwungenen Zustand!
Für den Füllstand des Tanks
Einmal differenzieren führt zu
Ersetzen von
Nun muss noch der
Eingesetzt in die Differentialgleichung von
b) Laplace-Transformation und Füllstand
Zunächst gilt es alle zeitlich veränderlichen Größen in den beiden Differentialgleichung in den Laplace-Bereich (Bildbereich) zu überführen. Mit Hilfe des Laplacschen Differentiationssatzes ergibt sich
Diese Terme werden in die beiden Differentialgleichungen eingesetzt womit sich die beiden Laplace-Transformierten der betrachteten Differentialgleichungen ergeben.
Um einen Ausdruck für den Füllstand
Gleichermaßen wird (2) nach
Nun wird (3) in (4) eingesetzt
Weiter auflösen führt auf den gesuchten Ausdruck für den Füllstand
Der Term stellt dann nicht nur den Term dar der den Füllstand
c) zeitlicher Verlauf des Füllstandes
Der in b) erhaltene Ausdruck für
Somit gilt
Setzt man in (5) die Angaben aus der Aufgabenstellung ein ergibt sich
Der erhaltene Term stellt damit die homogene Lösung der Differentialgleichung im Laplace-Bereich dar. Mithilfe der Laplace Korrespondez Tabelle kann der zeitliche Verlauf des Füllstandes