3 / 3

Aufgabenstellung:

Eine Brennstoffzelle ist eine elektrochemische Zelle, die die Reaktionsenergie eines kontinuierlich zugeführten Brennstoffes (z.B. Wasserstoff) und eines Oxidationsmittels (z.B. Sauerstoff bzw. Luft) in nutzbare elektrische Energie umwandelt. Bei dieser Reaktion entsteht neben Wasser als Reaktionsprodukt immer auch Wärme. Um ein Überhitzen der Brennstoffzelle zu vermeiden, muss die Reaktionswärme laufend abgeführt werden.

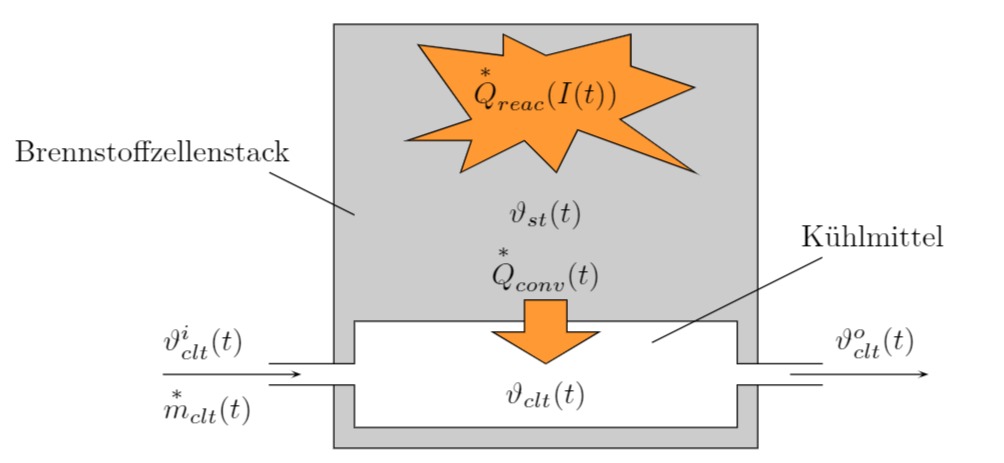
Abbildung

In dieser Aufgabe soll für einen wassergekühlten Brennstoffzellenstack (Serienschaltung mehrerer einzelner Brennstoffzellen) ein thermisches Modell erstellt und analysiert werden. Dazu werden die folgenden vereinfachenden Annahmen gemacht:

  • Reduktion auf zwei thermische Speicher (Brennstoffzellenstack, Kühlmittel)
  • Homogene Temperaturverteilung in den Speichern
  • Kein Wärmeverlust über die Oberfläche des Stacks an die Umgebung
  • Temperaturunabhängige Systemparameter

Weiter ist folgende Gleichung für die Reaktionswärme gegeben,

und angenommen, dass zwischen Stack und Kühlmittel ein konvektiver Wärmetransfer stattfindet,

Die Kühlmittelaustrittstemperatur soll gleich der Kühlmitteltemperatur gesetzt werden «perfect mixing"»,

 

Aufgabenstellungen

  1. Stellen Sie die Energiebilanzen (1. Hauptsatz) für die beiden thermischen Speicher auf und schreiben Sie das resultierende Differentialgleichungssystem 2. Ordnung an, mit:
  2. Berechnen Sie die Gleichgewichtswerte und analytisch in Abhängigkeit der Betriebspunktwerte .
  3. Linearisieren Sie das System um den Gleichgewichtspunkt und geben Sie die resultierenden Matrizen und an.

    Das konkrete System weise die folgenden Parameter- und Betriebspunktwerte auf:
  4. Werten Sie die Systemmatrizen und numerisch aus.
  5. Beurteilen Sie die Lyapunov-Stabilität des Systems.
  6. Ist das System vollständig steuerbar?
  7. Ist das System für und vollständig beobachtbar?
  8. Berechnen Sie die Übertragungsmatrix des linearisierten Systems vom Eingang auf den Ausgang .
  9. Welches Übertragungsverhalten wird durch den Eintrag der Übertragungsmatrix beschrieben? Geben Sie eine physikalische Interpretation der Ordnung und des statischen Übertragungsfaktors von .

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Energiebilanzen (1. Hauptsatz) und resultierendes Differentialgleichungssystem 2. Ordnung 

Wendet man den 1. Hauptsatz der Thermodynamik auf den Brennstoffzellenstack an, so ergibt sich die folgende Bilanz:

Die innere Energie des Brennstoffzellenstacks kann unter der Annahme einer konstanten spezifischen Wärmekapazität geschrieben werden als

Die beiden Wärmeströme sind in der Aufgabenstellung gegeben als

Setzt man die Beziehungen in die Bilanz ein, so resultiert die folgende Differentialgleichung:

Für das Kühlmittel lautet der 1. Hauptsatz,

Analog kann die innere Energie des Kühlmittels geschrieben werden als

Unter Vernachlässigung der kinetischen und der potentiellen Energie und unter der Annahme einer konstanten spezifischen Wärmekapazität ergibt sich für die Enthalpieströme des Kühlmittels,

beziehungsweise

Hinweis: In der letzten Gleichung wurde die Annahme des «perfect mixing", , ausgewertet.

Werden die Beziehungen eingesetzt, so ergibt sich

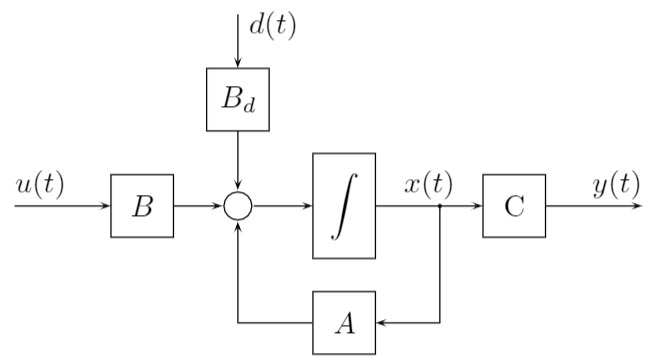
Mit den Definitionen für die Zustandsgrössen, die Eingansgrössen und die Störgrösse,

resultiert schliesslich das folgende Differentialgleichungssystem 2. Ordnung:

b) Gleichgewichtswerte und

Aus dem vorgegebenen Betriebspunkt (elektrischer Strom), (Betriebstemperatur) und (Kühlmittelmassenstrom) können die Gleichgewichtswerte für die Kühlmitteltemperatur und die Kühlmitteleintrittstemperatur bestimmt werden.

Ersetzt man , so erhält man für ,

c) Linearisierung um den Gleichgewichtspunkt und resultierende Matrizen und  

Linearisiert man das Differentialgleichungssystem um den Gleichgewichtspunkt , resultiert das folgende lineare System 2. Ordnung,

mit den Systemmatrizen

Bemerkung: und bezeichnen im linearisierten System die Abweichungen von den Betriebspunktwerten.

d) Numerische Auswertung von und

Mit den gegebenen numerischen Werten erhält man

e)  Lyapunov-Stabilität

Für die Beurteilung der Stabilität des Systems werden die Eigenwerte von , d.h. die Wurzeln des charakteristischen Polynoms berechnet,

mit den folgenden Koeffizienten :

Auflösen der quadratischen Gleichung ergibt die Eigenwerte zu

Beide Eigenwerte liegen in der linken Halbebene. Das System ist damit asymptotisch stabil.

f) vollständige Steuerbarkeit

Das System ist genau dann vollständig steuerbar, wenn die Steuerbarkeitsmatrix vollen Rang hat,

Vollständig steuerbar .

Im vorliegenden Fall ergibt sich für die Steuerbarkeitsmatrix:

Offensichtlich hat vollen Rang , womit das System vollständig steuerbar ist.

g) vollständige Beobachtbarkeit

Mit der in der Aufgabenstellung gegebenen Definition des Ausgangsvektors , lautet die Ausgangsgleichung des linearen Systems,

,

mit den Matrizen :

Bemerkung: bezeichnet den Vektor der Abweichungen von den Betriebspunktwerten, und .

Das System ist genau dann vollständig beobachtbar, wenn die Beobachtbarkeitsmatrix vollen Rang hat,

Vollständig beobachtbar

Im vorliegenden Fall lautet die Beobachtbarkeitsmatrix:

Offensichtlich hat vollen Rang , womit das System vollständig beobachtbar ist.

Bemerkung: Dass dieses System vollständig beobachtbar ist, lässt sich auch an der Ausgangsmatrix erkennen, die selbst schon Rang zwei hat, .

h) Übertragungsmatrix

Die Übertragungsmatrix eines MIMO-Systems wird analog zur Übertragungsfunktion eines SISO-Systems berechnet, mit:

Für das Modell des Brennstoffzellenstacks ergibt sich somit

Bemerkung: Die Übertragungsmatrix beschreibt das Übertragungsverhalten vom Eingang auf den Ausgang . Das Übertragungsverhalten von der Störgrösse auf den Ausgang lautet,

Abbildung

i) Physikalische Interpretation der Ordnung und des statischen Übertragungsfaktors von

Die Übertragungsfunktion

beschreibt das Übertragungsverhalten im linearisierten System (Abweichungen von den Gleichgewichtswerten!) von auf , hat 2. Ordnung und einen statischen Übertragungsfaktor von 1.

Physikalisch ergibt sich folgende Interpretation:

Ordnung:

Über die Kühlmitteleintrittstemperatur wird zuerst das Kühlmittelreservoir und erst mittelbar über den konvektiven Wärmeaustausch der Brennstoffzellenstack gekühlt. Es resultiert somit ein Verzögerungselement 2. Ordnung.

 

Statischer U̇bertragungsfaktor:

Der statische Übertragungsfaktor von 1 bedeutet, dass eine Temperaturänderung um am Kühlmitteleingang (statisch) nach «unendlich langer Beobachtungszeit»eine Änderung der Temperatur des Stacks um ebenfalls zur Folge hat.

Lösung:

  2. ,
  3. siehe Musterlösung 
  5. asymptotisch stabil
  6. vollständig steuerbar
  7. vollständig beobachtbar 

  9. siehe Musterlösung