1 / 3

Aufgabenstellung:

Leiten Sie für beide unten abgebildeten Masse- Feder-Dämpfer Systeme ein mathematisches Modell her und bestimmen Sie die Ruhelage des Systems. Gehen Sie dazu jeweils wie folgt vor:

  1. Identifizieren Sie die Energiespeicher ('reservoirs') und die zugehörigen Speichergrößen ('level variables').
  2. Identifizieren Sie Zu- und Abflüsse ('flows'). Überlegen Sie sich dazu welche Masseinheit diese Flüsse haben müssen.
  3. Formulieren Sie die Energiebilanzgleichungen für System A und B
  4. Bestimmen sie die Ruhelage des Systems aus den gewonnenen Differentialgleichungen.

Bemerkungen: Es wirke zusätzlich zur Erdbeschleunigung jeweils die externe Kraft auf die Masse . Die Länge der entspannten Feder beträgt

 

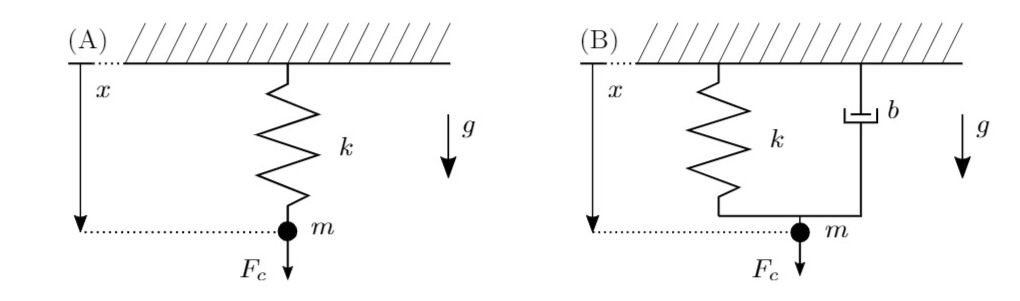
Masse Feder Dämpfer

 

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

1. In beiden Systemen gibt es drei Speicher:  

  • Kinetische Energie:
  • Potentielle Energie des Gravitationsfeldes:
  • Potentielle Energie der Feder:

Die im System gespeicherte Energie ist dann:

mit den 'level variables' und .

2. Die Energiebilanz lautet:

wobei in diesem Fall Zu- und Abfluss durch die mechanischen externen Leistungen (Masseinheit: W) gegeben sind. Die Zuflüsse für die Systeme und sind gleich: Zufluss

Die Abflüsse sind unterschiedlich:

  • : Abfluss  
  • : Abfluss

3. Somit wird die Energiebilanzgleichung für das System zu:

und für das System zu:

4. In der Ruhelage muss gelten: Somit werden die Gleichungen zu:

Die Ruhelage beider Systeme ist somit gleich.

Anmerkung: Die Anwendung des zweiten Newtonschen Gesetzes auf das System führt zum gleichen Ergebnis. Die oben beschriebene Vorgehensweise ist jedoch sehr allgemein gültig und kann bei sehr unterschiedlichen Systemen angewendet werden.

Lösung:

  2. siehe Musterlösung