Aufgabenstellung:
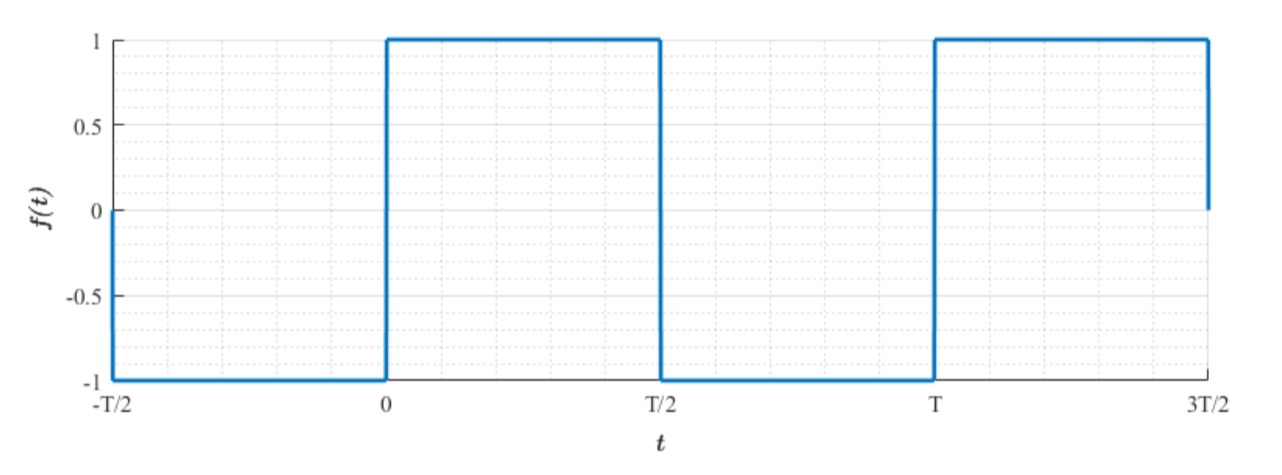
Man berechne die reelle Fourierreihe des in der Abbildung dargestellten periodischen Rechtecksignals. An den Sprungstellen nehme das Signal den Wert
Lösungsweg:
Für das Rechtecksignal in der Abbildung gilt
Es handelt sich also um eine ungerade Funktion mit
Mit
folgt schließlich (die Schreibweise
Die Fourierreihe lautet damit
Man erkennt, dass die Fourierreihe an den Stellen