Aufgabenstellung:
Die Auslenkung eines Körpers entspricht einer allgemein periodischen Schwingung der Form
- Zeichnen Sie die Funktion
. Ist die Funktion gerade oder ungerade? - Bestimmen Sie deren Gleichanteil
sowie die komplexen FOURIER-Koeffizienten. - Ist das resultierende Spektrum kontinuierlich oder diskret?
Zeichnen Sie das Amplitudenspektrum fürund .
Lösungsweg:
Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen
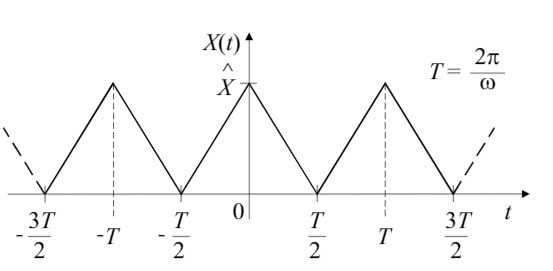
1. Zeichnen Sie die Funktion
Die Funktion ist gerade, da die Sinusanteile verschwinden
2. Bestimmen Sie deren Gleichanteil
Aus den reellen Koeffizienten
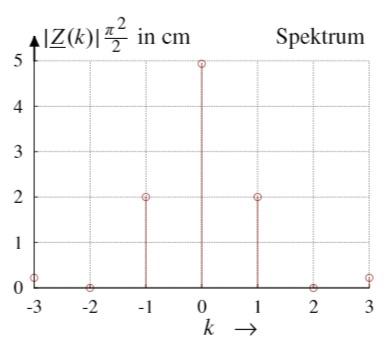
3. Ist das resultierende Spektrum kontinuierlich oder diskret?
Zeichnen Sie das Amplitudenspektrum für
Diskret, da
Lösung:
siehe Lösungsweg.