Aufgabenstellung:
Die Modellbildung einer physikalischen Anlage als gedämpftes Federpendel liefert bei äußerer Anregung
- Bestimmen Sie den komplexen Frequenzgang
, den Amplituden-Frequenzgang bzw. und den Phasen-Frequenzgang . - Berechnen Sie
und für die Stützwerte . Zeichnen Sie das BODE-Diagramm und kennzeichnen Sie die asymptotischen Verläufe durch Geraden. Bei welcher Kreisfrequenz ,,knicken“ Amplituden- und Phasengang ab? - Wie groß ist die stationäre Verstärkung
?
Lösungsweg:
1. Bestimmen Sie den komplexen Frequenzgang
Nach LAPLACE-Transformation für verschwindende Anfangsbedingungen folgt:
Der Frequenzgang
Mit den folgenden Ausdrücken für
2. Zeichnen Sie das BODE-Diagramm und kennzeichnen Sie die asymptotischen Verläufe
Nun kann der Amplituden- und Phasen-Frequenzgang skizziert werden:
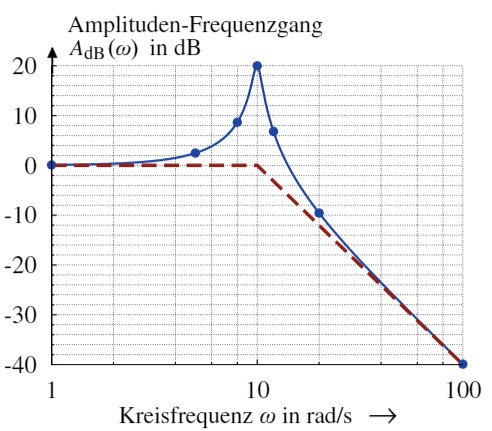
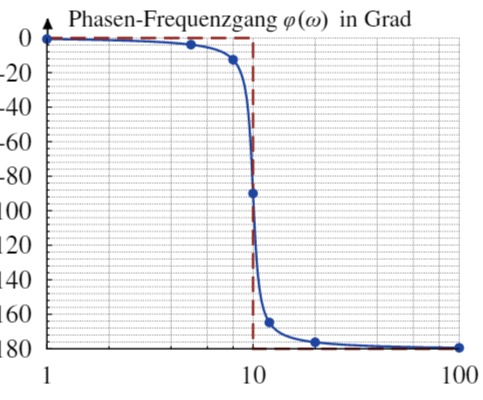
3. Wie groß ist die stationäre Verstärkung
Das gleiche Ergebnis folgt aus dem Endwertsatz der LAPLACETransformation, wenn für
Da auch
Auch aus der Schwingungsgleichung selbst kann dies abgelesen werden, da im stationären Fall
Lösung:
- siehe Lösungsweg
- siehe Lösungsweg