Aufgabenstellung:
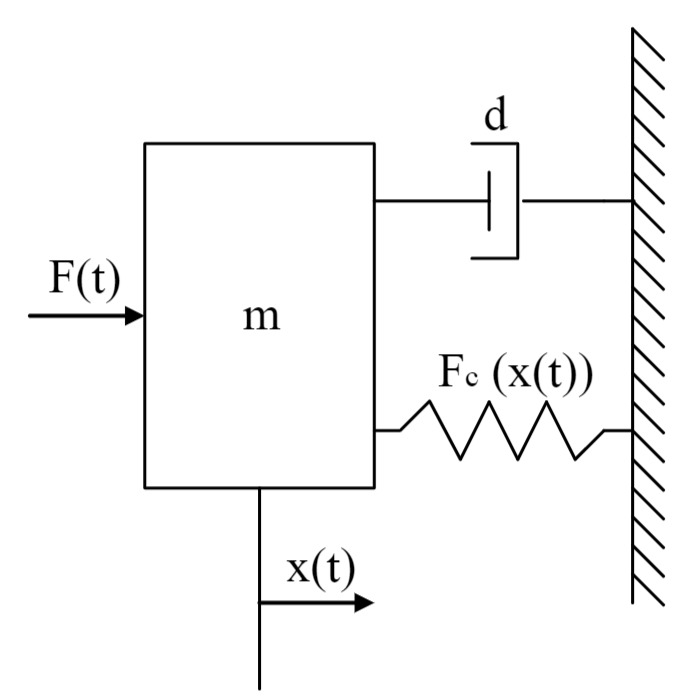Gegeben ist das dargestellte Feder-Masse-Dämpfer System aus der ersten Übung. Die Feder wurde durch ein anderes Modell ersetzt, und besitzt nun eine nichtlineare Kennlinie der Form
- Bestimmen Sie die Differentialgleichung, die die Dynamik des oben dargestellten Feder-Masse-Dämpfer Systems mit der neuen Feder in der Koordinate
beschreibt. - Linearisieren Sie die erhaltene Differentialgleichung um deren Ruhelage bei einer konstanten Anregung
.
Lösungsweg:
a) Differentialgleichung des Feder-Masse-Dämpfer Systems
Die Federkraft des Systems kann durch die folgende Gleichung beschrieben werden
Die allgemeine DGL des Systems lautet:
eingesetzt mit der Federkraft ergibt sich:
b) Linearisierung der Differentialgleichung
Durch die nichtlineare Federkennlinie wird das System nun durch eine nichtlineare inhomogene DGL beschrieben. Diese soll jetzt im Folgenden in einer Ruhelage linearisiert werden.
Für die Ruhelage gilt:
- System ist in Ruhe, keine Bewegungen mehr vorhanden:
- System wird mit einem konstanten
angeregt
Eingesetzt in die DGL ergibt sich
Die Gleichung wird nach
In dieser Ruhelage wird die DGL durch ein lineares Modell angenähert, welches Abweichungen des Systems von dieser Ruhelage beschreibt.
Hierzu werden die zeitabhängigen Größen in der DGL durch die folgenden Ausdrücke ersetzt:
Diese Ausdrücke werden in (1) eingesetzt
Es zeigt sich, dass für die linearen Ausdrücke der beiden Ableitungen von
Es ergibt sich der nichtlineare Ausdruck
Der nichtlineare Ausdruck wird nun durch eine Taylorreihen-Entwicklung linear angenähert. Hierzu wird der ursprüngliche nichtlineare Ausdruck aus der ursprünglichen DGL durch eine Taylorreihe entwickelt und nach dem linearen Glied abgebrochen
Angewandt auf das hier vorliegende Problem ergibt sich
Durch Einsetzen von
eine Approximation des nichtlinearen Terms.
Wird diese Approximation nun in (2) eingesetzt, erhält man die lineare Differentialgleichung
die gewünschte lineare Differentialgleichung approximiert die DGL (1) in der Umgebung der Ruhelage