4 / 5

Aufgabenstellung:

Die Skizze zeigt einen 1-Massenschwinger, bestehend aus der Masse , linearer Feder mit der Steifigkeit und linearem Dämpfer mit dem Koeffizienten . Das System befinde sich in der Ruhelage, das heißt Gewichtskraft und Federkraft sind ausgeglichen.

Konstanten

Masse

Federkonstante

Dämpfungskonstante


Variablen

Kraft

Weg, Auslenkung aus der Ruhelage

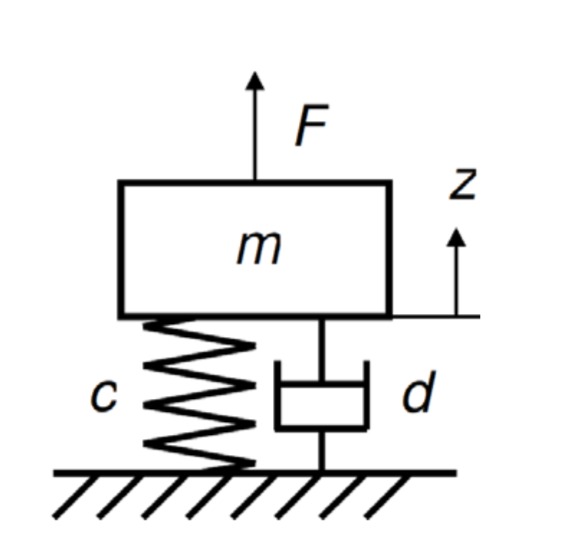
Abbildung

  1. Stellen Sie die Differentialgleichung für den Weg in Abhängigkeit der Kraftanregung auf.

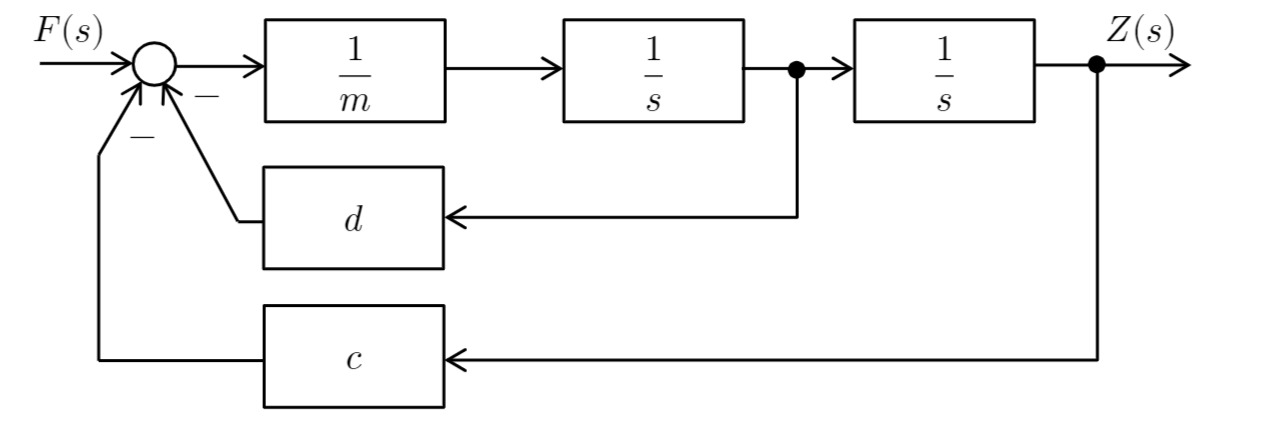
  2. Zeichnen Sie den linearen Signalflussplan.

  3. Bestimmen Sie die Übertragungsfunktion  

  4. Bestimmen Sie die Pol- und Nullstellen des Systems für und 

  5. Berechnen und skizzieren Sie die Sprungantwort des Systems! Zum Zeitpunkt ist das System in Ruhe und die Kraft wird angelegt. Sie nimmt sprungförmig den Wert an.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Differentialgleichung 

Aufstellen der linearen Differentialgleichung

Kräftegleichgewicht:

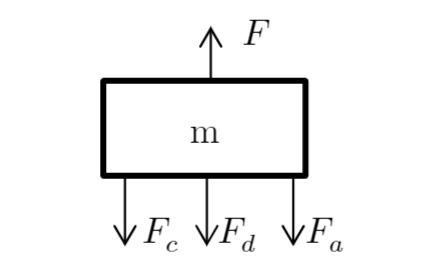
Abbildung

Mit der Federkraft ,  der Dämpferkraft und der Trägheitskraft folgt:

b) Signalflussplan

Auflösen nach der höchsten Ableitung von :

Aufstellen des Signalflussplans/Blockschaltbild/Wirkungsplans:

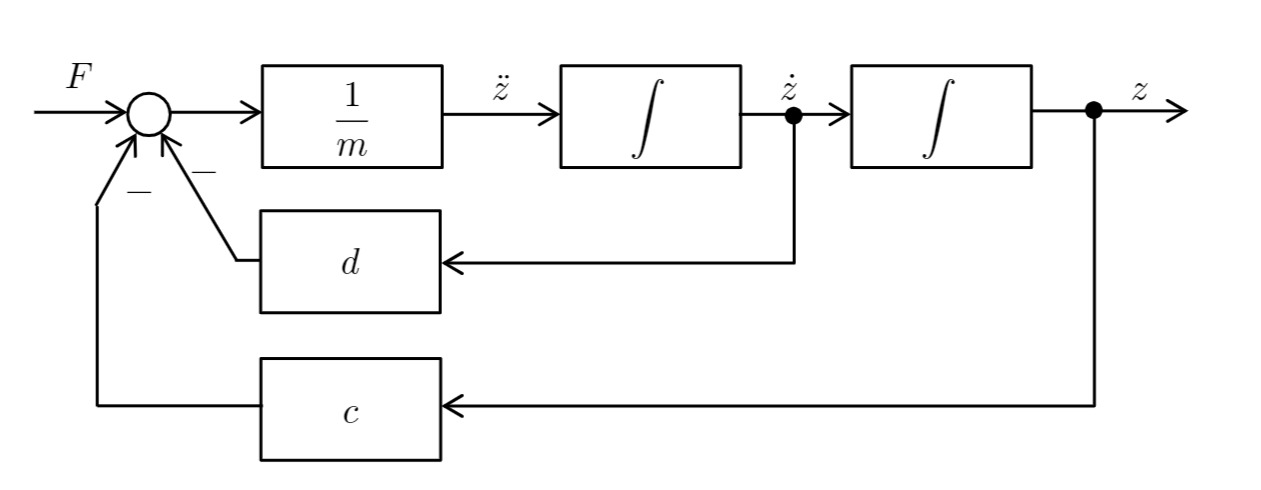
Abbildung

Transformation in den Bildbereich:

Abbildung

c) Überstragunsfunktion 

Zusammenfassen der inneren Rückkopplung :

Abbildung

Zusammenfassen der äußeren Rückkopplung :

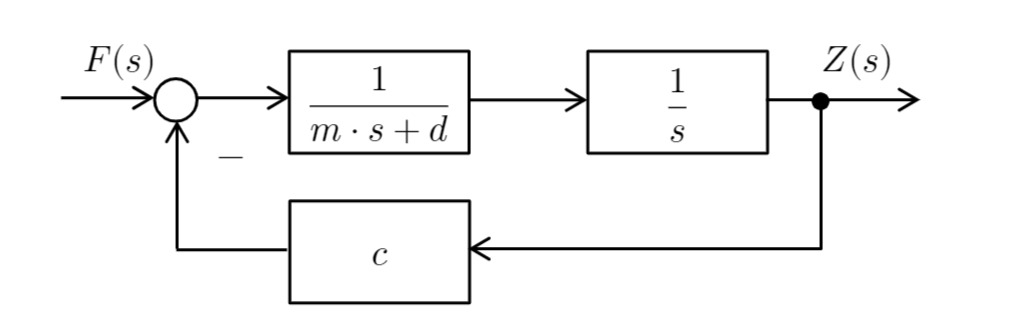
Abbildung

Normierung (nicht notwendig):

ü

d) Pol-und Nullstellen: 

Nullstellen:

Polstellen:

Skizze Pol- und Nullstellen (optional): 

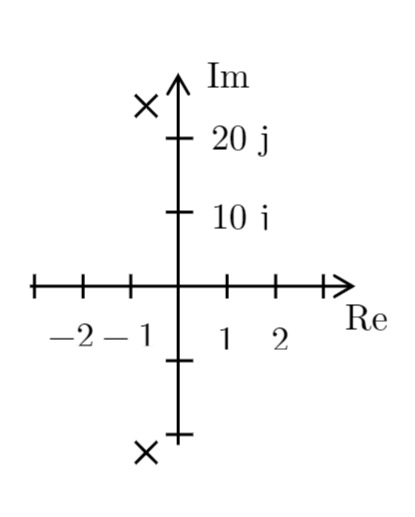
Abbildung


e) Sprungantwort:

Normierte Übertragungsfunktion

Eingangangssprung

Lösung der Differentialgleichung im Bildbereich:

Koeffizientenvergleich mit

mit den Formeln und  ergeben sich und zu:

Das ergibt die Abklingtkonstante , die gedämpfte Eigenkreisfrequenz und die Phasenverschiebung

Damit kann die Lösung der Differentialgleichung im Zeitbereich aufgestellt werden:

Die Differentialgleichung ergibt sich aus der allgemeinen Form multipliziert mit der Sprunghöhe

Skizze :

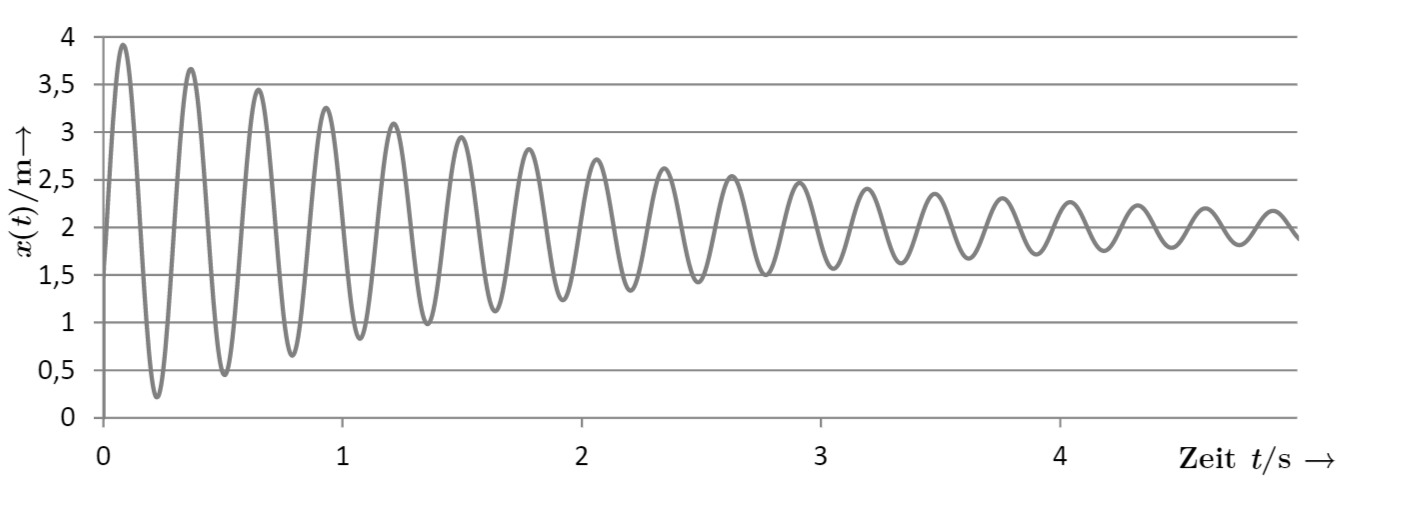
Abbildung

Lösung:

  2. Abbildung

  4. ;