2 / 5

Aufgabenstellung:

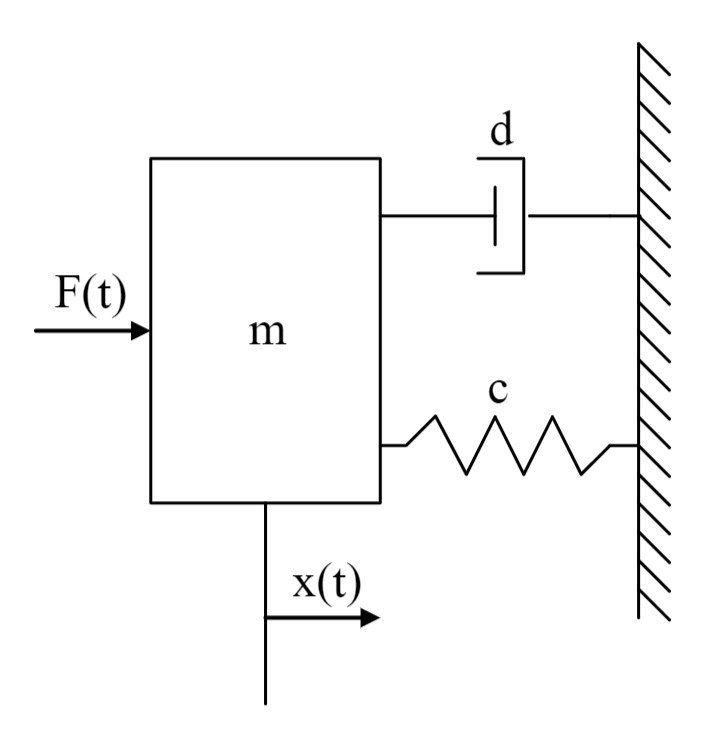AbbildungGegeben ist das dargestellte System mit der Masse , einem linearen Dämpfer mit der Dämpferkonstante und einer linearen Feder mit der Steifigkeit . Das System wird von einer zeitabhängigen Kraft angeregt.

 

a) Bestimmen Sie die Differentialgleichung, welche die Bewegung der Masse in -Richtung des dargestellten Systems in Abhängigkeit der angreifenden Kraft beschreibt.
b) Ist das erhaltene System linear?

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Differentialgleichung

Zunächst wird die Masse freigeschnitten und alle an der Masse wirkenden Kräfte aufgestellt. Diese ergeben sich zu:

ä

Damit ergibt die Summe aller wirkenden Kräfte zu

Zusätzlich gilt , sodass sich die Differentialgleichung (DGL) des Feder-Masse-Dämpfer Systems ergibt:

 Nun wird die DGL noch umgestellt um Eingänge und Ausgänge zu trennen

b) Linearität prüfen

Ein dynamisches System ist genau dann linear, wenn das Superpositionsprinzip gilt. Das bedeutet, dass linear überlagerte Eingangssignale zu linear überlagerten Ausgangssignalen führen. Es gilt also zu prüfen, ob aus einem auch folgt.

Es gilt für und

Weiterhin gilt

Somit ergibt sich für

Die Bedingung ist somit erfüllt und die DGL linear.

Allgemeiner Hinweis:

Allgemein gilt, dass eine lineare DGL immer die Form besitzt

wobei mit der Systemausgang und mit der Systemeingang bezeichnet wird. Es gilt weiterhin, dass die Koeffizienten und konstant sind und . Das bedeutet, dass alle zeitabhängigen Größen nur in der ersten Ordnung vorliegen und diese nur addiert werden. Multiplikationen können nur mit konstanten Koeffizienten vorliegen. Daraus folgt, das sämtliche anderen mathematischen Operationen wie oder nichtlinear sind.

Lösung:

  2. System ist linear