Aufgabenstellung:
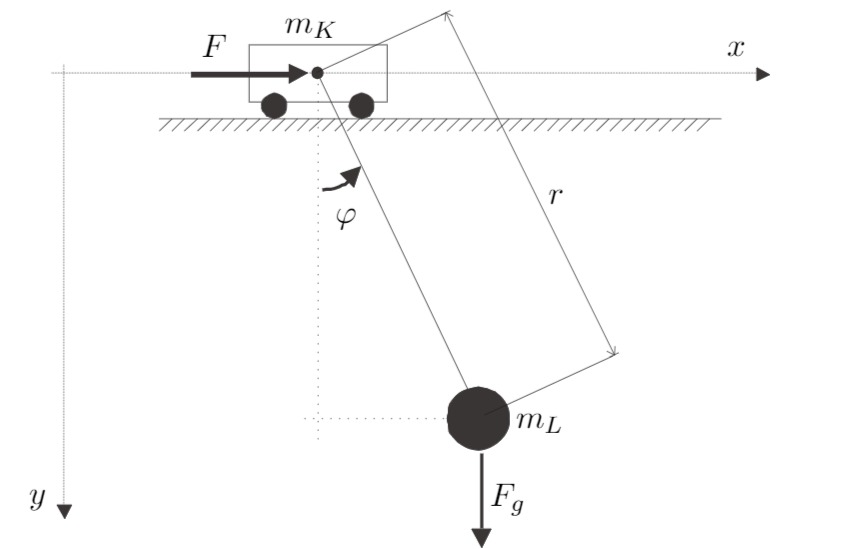Gegeben ist die in der Abbildung gezeigte Verladebrücke, für die ein mathematisches Modell erstellt werden soll. Die Last
Schwerpunkt der Laufkatze mit der Masse
Die Durchbiegung des Seils kann vernachlässigt werden, da nur kleine Seilwinkel
- Bestimmen Sie die Bewegungsgleichungen der Verladebrücke mit Hilfe der Newtonschen Gesetze.
- Linearisieren Sie die Bewegungsgleichungen um die stabile Gleichgewichtslage für kleine Winkelgeschwindigkeiten
, und geben Sie das linearisierte System in Zustandsdarstellungl an. Wählen Sie dabei den Zustandsvektor .
Lösungsweg:
a) Bewegungsgleichung
Die Verladebrücke besteht aus zwei mechanischen Teilsystemen, die durch ein Seil miteinander gekoppelt sind.
Es bietet sich an die Systeme getrennt zu betrachten, wobei dann die sogenannte Schnittkraft
Es resultieren die Kräfte (Skizze und Gleichungen)
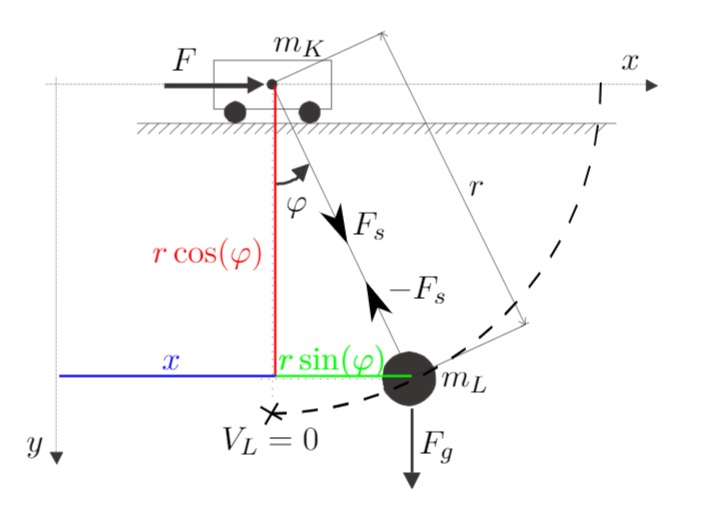
Die Kraftbilanzen für die beiden Teilsysteme werden für die
Laufkatze:
Die Beschleunigung des Schwerpunktes der Laufkatze ergibt sich zu
Last:
Die Beschleunigung des Schwerpunktes der Last ergibt sich zu:
Zusammenfassend erhält man für die Laufkatze
Für die Last gilt:
Aus dem Gleichungssystem erhält man gekoppelte Bewegungsgleichungen.
Stellt man (3) nach
Die 2. Bewegungsgleichung erhalten wir, wenn
Die gekoppelten Bewegungsgleichungen müssen nun entkoppelt (d.h. die höchsten Ableitungen isoliert auf die linke Seite gebracht) werden.
Dies wird nun in die 2. Bewegungsgleichung eingesetzt
Um das DGL-System in ein System 1. Ordnung zu überführen definieren wir die folgenden Zustände
Somit lassen die Bewegungsgleichung schreiben als
b) Linearisierung
Bemerkung:
Mathematisch betrachtet ist für den Winkel jedes Vielfache
Mit den Ausgängen