4 / 5

Aufgabenstellung:

Gegeben sind die beiden linearen Systeme

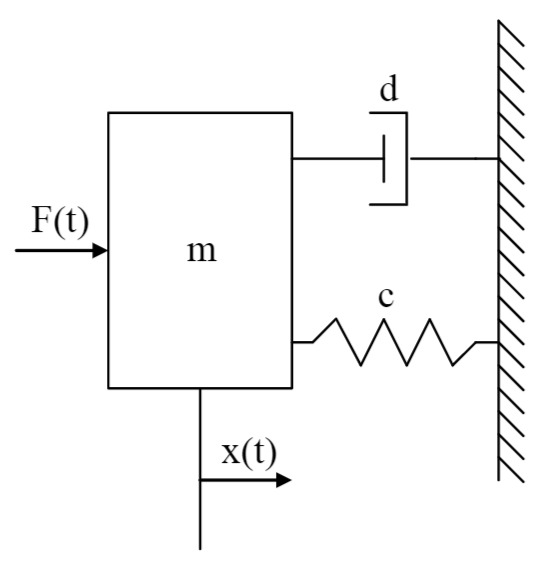
Abbildung

Abbildung a): Feder-Masse-Dämpfer System

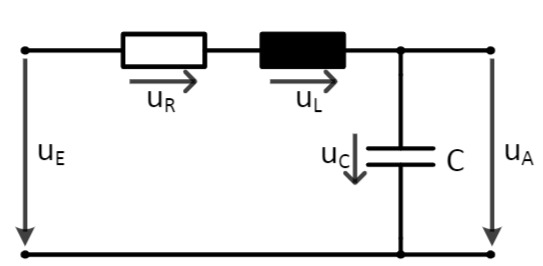
Abbildung

 Abbildung b): Elektrisches Netzwerk

Das System in Abbildung a) wurde bereits in der ersten Übung behandelt und wird mit der Differentialgleichung

(1)

beschrieben. Der in Abbildung b) dargestellte Schaltkreis besteht aus einem Widerstand , einer Induktivität und einer Kapazität . Der Schaltkreis wird mit einer Eingangsspannung von beaufschlagt und es fällt eine Spannung am Ausgang an.

  1. Bestimmen Sie die Differentialgleichung die das Ausgangsverhalten des in b) dargestellten Schaltkreises in Abhängigkeit von der Eingangsspannung beschreibt.
  2. Vergleichen Sie die erhaltene Differentialgleichung mit der in (1) beschriebenen Differentialgleichung des mechanischen Systems.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Differentialgleichung

Es gilt

Bauteilgleichungen:

Aufstellen der Maschengleichungen (2. Kirchhoffsches Gesetz) ergibt

Auflösen und Umformen des Gleichungssystems

Aufgrund von (3) und der Bauteilgleichung des Kondensators gilt

Einsetzen der Bauteilgleichungen in (2) ergibt

Aus (4) folgt weiterhin

Einsetzen von (3) und (6) in (5) ergibt

Daraus folgt unmittelbar

Umformen der Differentialgleichung des elektrischen Systems führt zu

b) Vergleich mit der Differentialgleichung aus der ersten Aufgabe

  • Beide Differentialgleichungen vom selben Typ (linear, inhomogen, zweiter Ordnung)
  • Identischer Aufbau
  • Durch Koeffizientenvergleich des homogenen Teils der DGL lässt sich die Elektro-MechanischeAnalogie herleiten
    • Masse - Induktivität
    • Dämpfungskoeff. - ohm. Widerstand
    • Federnachgiebigkeit - Kapazität

Die beiden Differentialgleichungen lassen sich in eine allgemeine Form

überführen.

  • Form tritt in der Regelungstechnik sehr oft auf
  • Viele technische Systeme besitzen (oder näherungsweise) dieses Verhalten
  • Wird auch als -Verhalten bezeichnet

Zur Erarbeitung allgemeinener Kenngrößen dieser Art von Differentialgleichungen wird (7) in eine andere Schreibweise überführt

Aus dieser Form lassen sich die beiden elementaren Kenngrößen von Differentialgleichungen mit -Verhalten direkt ermitteln.

  • Dämpfungsgrad (dimensionslos)
  • Eigenfrequenz

Es gilt zu beachten, dass der Dämpfungsgrad nicht mit dem linearen Dämpfungskoeff. bei einem mechanischen System gleichzusetzen ist, sondern eine allgemeine Systemeigenschaft darstellt. Diese lässt sich für alle technischen Systeme, welche -Verhalten aufweisen, bestimmen.

Zur Bestimmung der Kennwerte für die beiden vorher behandelten Differentialgleichungen werden beide in die in (8) dargestellte Form überführt

Für das mechanische System ergibt sich durch Koeffizientenvergleich 

Analog ergibt sich für das elektrische System:

Bei Vergleich der Kennwerte lässt sich ebenfalls die oben hergeleitete Analogie zwischen mechanischen und elektrischen Systemen erkennen, da durch das jeweilige Ersetzen der äquivalenten physikalischen Größen sich die Kenngrößen ineinander überführen lassen.

Mit Hilfe des Dämpfungsgrades lassen sich zusätzlich noch Aussagen über das Zeitverhalten des Ausgangs treffen.

  • Dämpfungsgrad aperiodisches Verhalten
  • Dämpfungsgrad aperiodischer Grenzfall
  • Dämpfungsgrad gedämpften Schwingung
  • Dämpfungsgrad ungedämpfte, instabile Schwingung

Diese Eigenschaften lassen sich auf die Eigenwerte des Systems zurückführen. Hierzu wird das charakteristische Polynom von (8) gebildet, was die folgenden beiden Lösungen besitzt

Die beiden Lösungen in entsprechen demnach den Eigenwerten von .

Betrachtet man nun die vorher aufgeführten Fälle für den Dämpfungsgrad, ergeben sich folgende Aussagen über die Beschaffenheit der Eigenwerte

  • Aperiodisches Verhalten bei zwei reellen Eigenwerten
  • Aperiodischer Grenzfall, ein doppelter Eigenwert
  • : Gedämpfte Schwingung bei einem komplex konjugiertem Polpaar mit negativem Realteil
  • : \quadUngedämpfte, instabile Schwingung bei einem komplex konjugiertem Polpaar mit positiven Realteil

Es zeigt sich also, dass man aufgrund der Beschaffenheit der Eigenwerte eine Differentialgleichung mit -Verhalten auf das Zeitverhalten der Ausgangsfunktion schließen kann. Insbesondere der letzte Fall soll hier hervorgehoben werden, da Eigenwerte mit positivem Realteil (oder positive reelle Eigenwerte) immer ein instabiles Systemverhalten beschreiben.

Lösung:

  2. siehe Musterlösung