In dieser Aufgabe werden Sie das System in der Abbildung analysieren. Sie werden die Regelstrecke (Elektromotor und Getriebe) modellieren. Ihr Modell werden Sie dann mit einem (P-)Regler zu einem Regelsystem erweitern. Die folgende Abbildung zeigt eine schematische Darstellung der Regelstrecke.

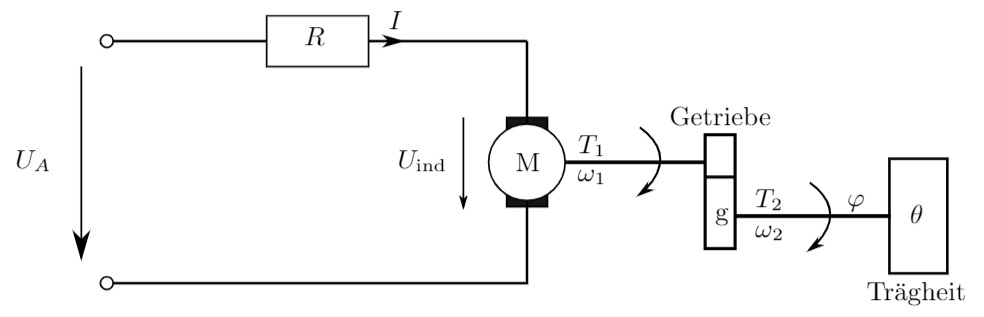
Die Eingangsgrösse der Regelstrecke ist die Ankerspannung Für den Ankerkreis des Elektromotors gilt das Kirchhoffsche Gesetz:

Die induzierte Spannung hängt von der Rotationsgeschwindigkeit des Motors ab. Wir nehmen an, dass dieser Zusammenhang wie folgt linear ist:

Wir nehmen auch an, dass das Drehmoment des Motors von der Stromstärke linear abhängt:

Für das Getriebe mit dem Übersetzungsverhältnis gilt (idealisiert ohne Reibung):

Der Drallsatz für den Motor liefert:

Verwenden Sie folgende Zahlenwerte für diese Aufgabe:

Aufgabenstellungen

a) Leiten Sie die Differentialgleichung her.

b) Leiten Sie ein Zustandsraummodell für das gegebene System her. Verwenden Sie als Zustandsvariablen die Geschwindigkeit und die Position auf der Abtriebsseite des Getriebes. Der Ausgang des Systems ist der Winkel .

c) Leiten Sie aus der Zustandsraumdarstellung die Übertragungsfunktion her. (Eine Übertragungsfunktion beschreibt den den Einfluss vom Eingang auf den Ausgang des Systems. Im gegebenen Fall ist der Eingang und der Ausgang )

Nun wird die Regelstrecke mit einem P-Regler zu einem Regelsystem erweitert. Der Sollwert wird mit dem Istwert verglichen und die Differenz der beiden in den P-Regler geführt. Der Ausgang des Reglers ist die Spannung . Diese Spannung wird im Elektronikteil (Verstärker) zur Ankerspannung umgewandelt. Da der Regler digital realisiert ist, muss mit einer kleinen Verzögerung gerechnet werden. Diese Verzögerung zwischen und soll mit einer Totzeit modelliert werden.

d) Wie lautet die Übertragungsfunktion für die Kreisverstärkung ?
e) Werten Sie das Nyquist-Kriterium aus. Welche Eigenschaften muss die Kreisverstärkung aufweisen, damit der geschlossene Regelkreis asymptotisch stabil ist? Sind diese Anforderungen erfüllt?

a) Differentialgleichung

e) Nyquist-Kriterium