Aufgabenstellung:
Abbildung 1.1 zeigt den Ankerkreis einer fremderregten Gleichstrommaschine mit variabler Ankerspannung
Dabei stellen
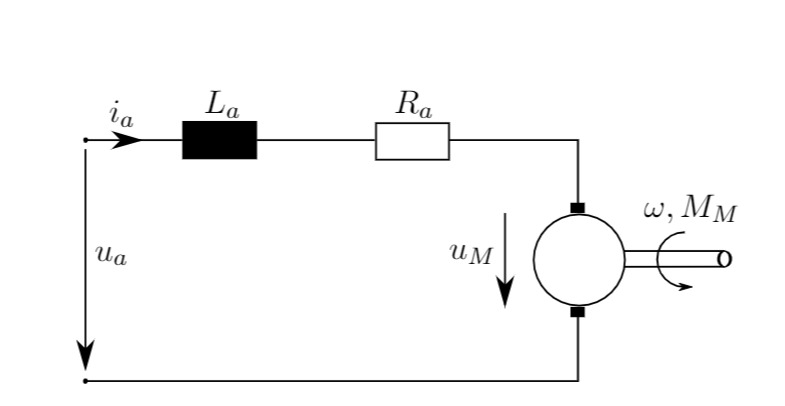
Abb. 1.1: Ersatzschaltbild des Gleichstrommotors.
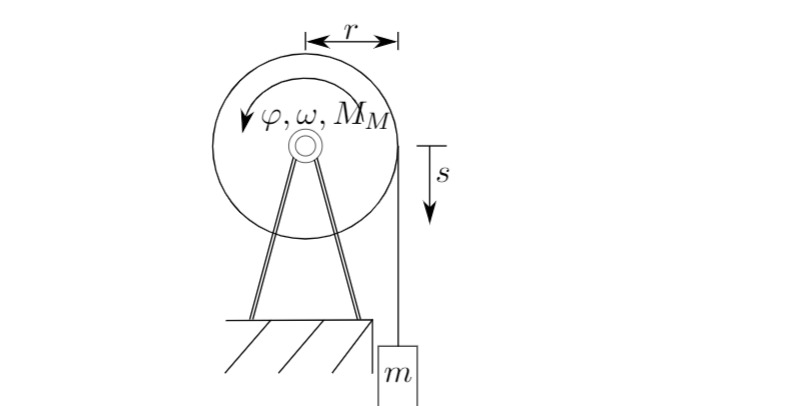
Abb. 1.2: Seilzug.
Die Gleichstrommaschine treibt den in Abbildung
Neben der auf die Masse
beschrieben wird. Es wird angenommen, dass das Seil dehnungsfrei ist und seine Dynamik vernachlässigt werden kann.
Hinweis: Für den skalaren Fall gilt, dass das Drehmoment das Produkt aus Kraft und Hebelarm ist.
a) Wählen Sie geeignete Eingangs-, Zustands- und Augangsgrößen und stellen Sie das mathematische Modell des Gesamtsystems in der Form
auf.
b) Welche stationäre Eingangsgröße
c) Linearisieren Sie das System um den Arbeitspunkt aus (b) und stellen Sie es wie folgt dar:
Lösungsweg:
a) Aufstellen des mathematischen Modells
Eingangsgröße:
Ausgangsgröße:
Die Regelstrecke besteht aus einem elektrischen Teilsystem (Gleichstrommaschine) und einem mechanischen Teilsystem (Seilwinde).
Für das elektrische System gilt nach dem Ersatzschaltbild (Abbildung 1.1) mittels der Maschengleichung
Die Bewegungsgleichung für das mechanische Teilsystem kann direkt aus dem Drehimpulserhaltungssatz hergeleitet werden:
Die Zeitabhängigkeit der Seillänge erhält man durch Differenziation der gegebenen Gleichung
Aus den obigen Gleichungen kann man eine Wahl für die Zustandsgrößen treffen, z.B.
Da als Ausgang
Zusammenfassend erhält man die Systembeschreibung mittels der Zustandsdarstellung
b)
In der Ruhelage gilt, dass keine Zustandsänderung erfolgt, d.h.
Somit gilt das folgende Gleichungssystem
Bemerkung:
Physikalisch gilt, dass
Es ergibt sich die eindeutige Lösung
c) Linearisierung
Nach Einführung der Variablen