5 / 6

Aufgabenstellung:

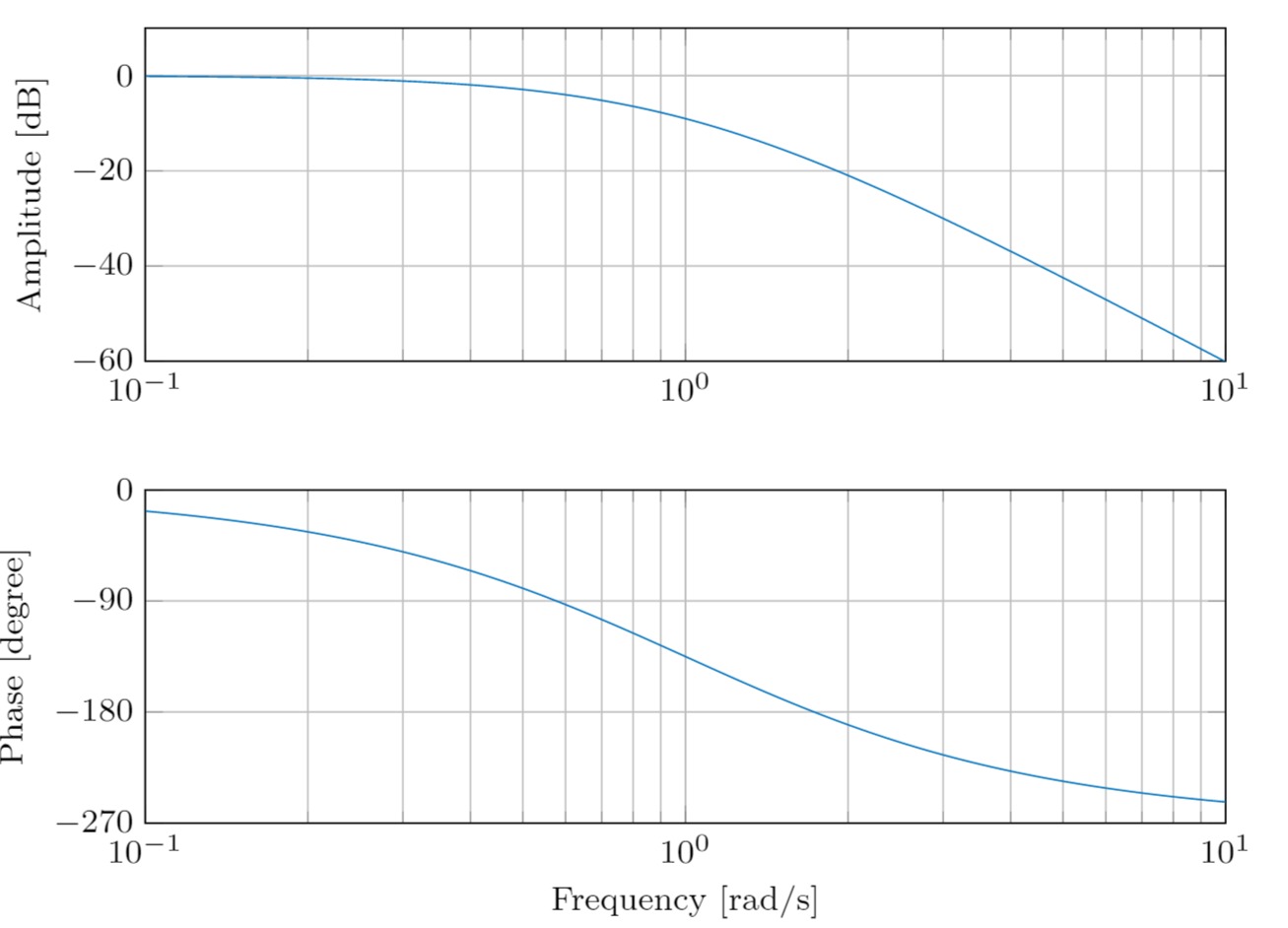
Von einer Strecke ohne Regler haben Sie das Bode-Diagramm in der Abbildung gegeben.

Abbildung

a) Finden Sie die kritische Frequenz , die kritische Verstärkung und . Berechnen Sie mit den Einstellregeln von Ziegler/Nichols die Parameter für den PI-Regler.

Nachdem Sie die Parameter des Reglers bestimmt haben, sagt Ihr Kollege, dass das gegebene Bode-Diagramm falsch war. Er hat die Strecke nun richtig modelliert und gibt Ihnen die Übertragungsfunktion an:

Er möchte nun, dass Sie einen PID-Regler auslegen.

b) Berechnen Sie die Ziegler/NicholsParameter des PID-Reglers analytisch für die neue Strecke.

Lösungsweg:

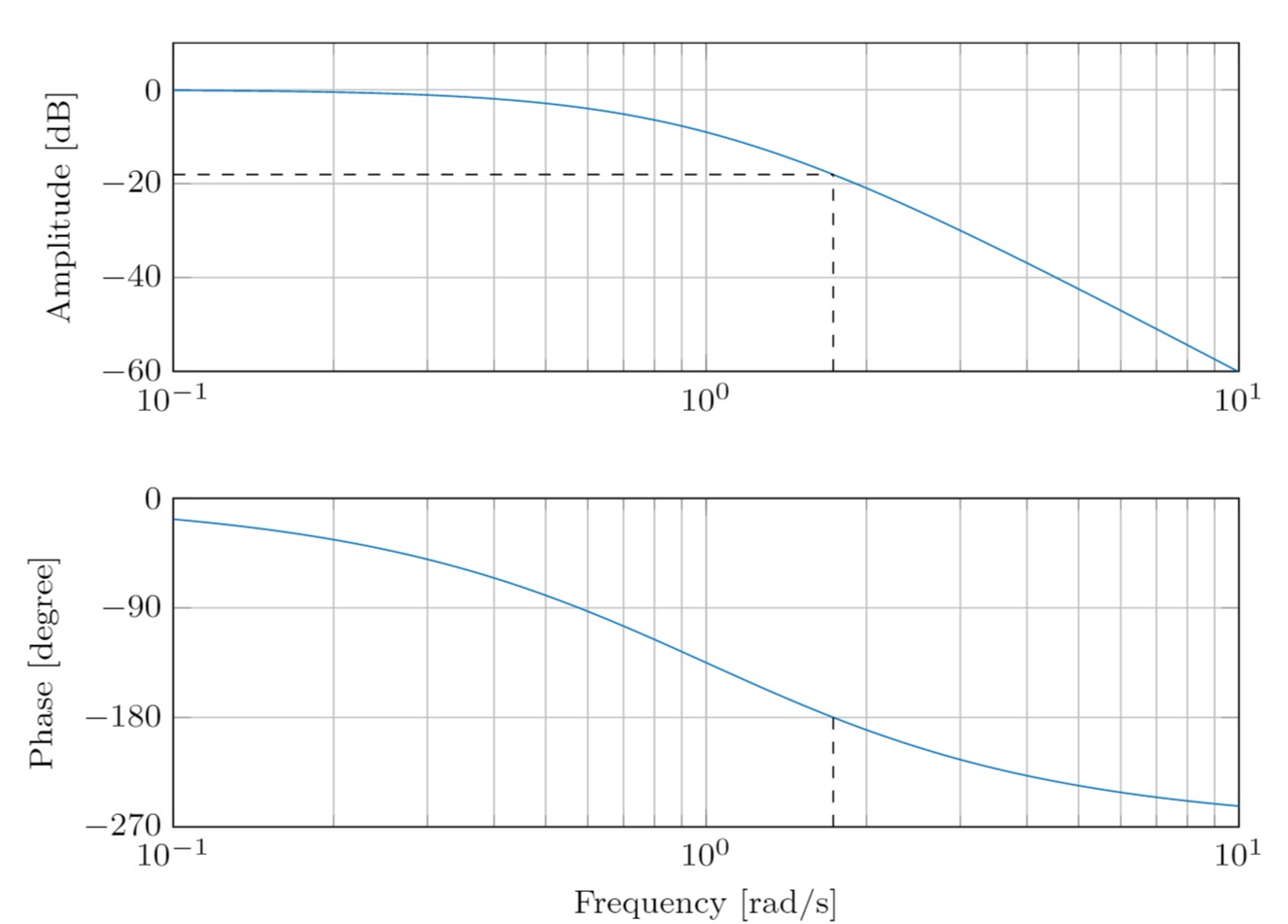
Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) , und ;  

Die Parameter wird bei aus dem Bode-Diagramm der Strecke ausgelesen (siehe Abb.):

Somit ergibt sich für :

Die Amplitude bei der Frequenz beträgt . Somit kann auch die kritische Verstärkung bei aus dem Bode-Diagramm der Strecke bestimmt werden (siehe Abb.):

Die Parameter für den PI-Regler nach Ziegler/Nichols sind:

Der Regler hat die folgende Übertragungsfunktion:

Abbildung

b) Ziegler/NicholsParameter

Um die Ziegler/Nichols-Parameter analytisch zu bestimmen, muss als erstes die kritische Verstärkung und die kritische Periode berechnet werden. Die kritische Periode befindet sich im Nyquist-Diagramm bei demjenigen Punkt, bei dem die Nyquistkurve des Systems die reelle Achse schneidet und von allen möglichen Schnittpunkten derjenige Punkt ist, welcher am nächsten beim kritischen Punkt liegt.

Potentielle Werte für die kritische Frequenz erfüllen die Gleichung:

oder

Für das gegebene System folgt somit:

Diese nichtlineare Gleichung für , kann nicht analytisch gelöst werden. 

Folglich ist die kritische Periode :

Die kritische Verstärkung berechnet man mit:

Die Parameter für den PID-Regler nach Ziegler/Nichols sind:

Der Regler hat die folgende Übertragungsfunktion:

Lösung: