4 / 6

Aufgabenstellung:

Gegeben ist das folgende System in Blockschaltbild-Form

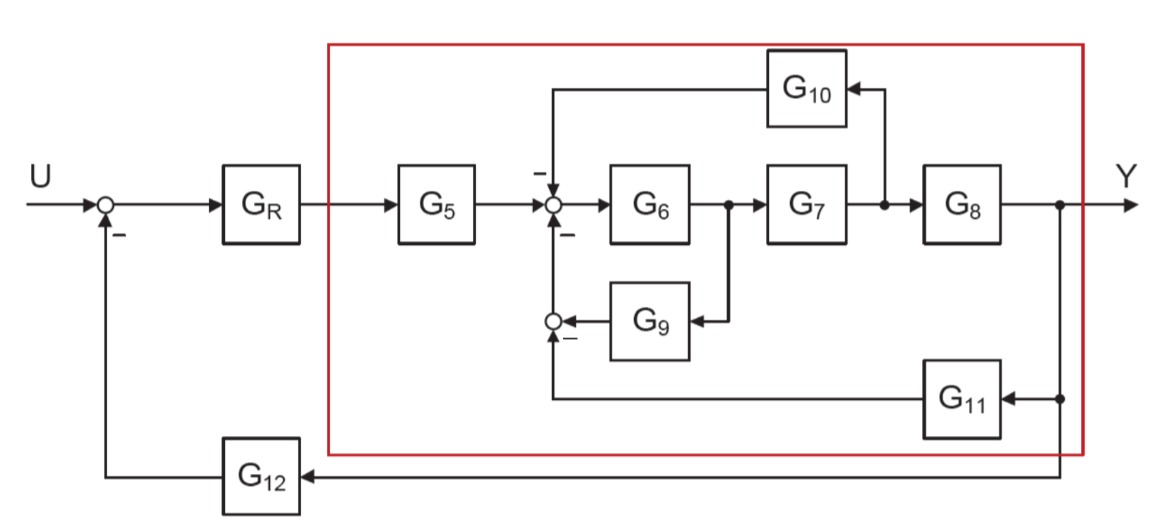
Abbildung

mit den allgemeinen Übertragungsfunktionen sowie . Für die Übertragungsfunktionen gilt:

a) Fassen Sie das in dem roten Kasten dargestellte Übertragungssystem zu einer doppelbruchfreien Übertragungsfunktion zusammen.
b) Prüfen Sie mit ob die Übertragungsfunktion stabil ist.

Das System wird nun mit einem Regler geregelt. Zusätzlich ist zur Betrachtung des Sensorverhaltens die Übertragungsfunktion in der Rückführung enthalten.

c) Stellen Sie die Gesamtübertragungsfunktion in doppelbruchfreier Form in Abhängigkeit von auf.

d) Ist das System mit einem P-Regler für ein stabilisierbar? Falls ja, bestimmen sie mit Hilfe des Hurwitz-Kriteriums den Bereich für in Abhängigkeit von , für den der geschlossene Regelkreis asymptotisch stabil ist.
e) Das System wird nun mit einem geregelt und mit einem Einheitssprung beaufschlagt. Es stellt sich ein stationärer Endwert von ein. Bestimmen Sie .
f) Der Regler soll nun mit dem Verfahren nach Ziegler-Nichols ausgelegt werden. Hierbei sollen sowohl ein P-, PI- als auch ein PID-Regler betrachtet werden. Bei einem Schwingversuch wurde an der oberen Stabilitätsgrenze eine Periodendauer von gemessen.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Doppelbruchfreie Übertragungsfunktion

Zunächst wird der relevante Teil des Blockschaltbildes (in der Abbildung rot markiert) umgestellt:

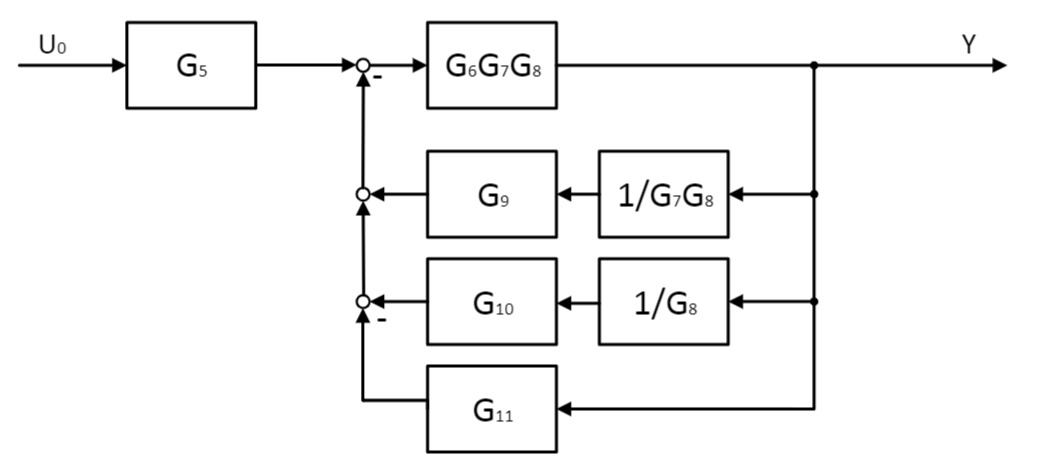
Abbildung

Nun lässt sich das System mit den Regeln zusammenfassen. Die Übertragungsfunktion wird mit der oben dargestellten Parallelschaltung aus den drei Reihenschaltungen rückgekoppelt. Das dabei entstehende System liegt dann noch mit in Reihe geschaltet vor.

Somit lässt sich die gesuchte Übertragungsfunktion sehr einfach aufstellen

b) Stabilität der Übertragungsfunktion

Durch Einsetzen der gegebenen Übertragungsfunktionen für ergibt sich

Bei Betrachtung der Koeffizienten des Nennerpolynoms wird sofort klar, dass die notwendige Bedingung eines Hurwitz-Polynoms nicht erfüllt ist, da nicht alle Koeffizienten das gleiche Vorzeichen haben ( ist negativ). Das System ist somit instabil.

c) Gesamtübertragungsfunktion in doppelbruchfreier Form in Abhängigkeit von

Für die gesamte Übertragungsfunktion gilt

In diesem Fall ergibt sich für und

Eingesetzt in (1) ergibt für den Nenner

Damit ergibt sich die gesuchte Übertragungsfunktion zu

d) Stabilität mit einem P-Regler für ein ; Bereich für für den der geschlossene Regelkreis asymptotisch stabil ist

Damit ein System stabilisierbar ist, muss durch den Regler und die Rückkopplung das Nennerpolynom der Gesamtübertragungsfunktion so verändert werden können, dass dessen Nullstellen, also die Polstellen der Übertragungsfunktion, alle negative Realteile besitzen. Im Kontext der algebraischen Stabilitätskriterien bedeutet dies, durch die Regelung muss das Nennerpolynom der Übertragungsfunktion in ein Hurwitz-Polynom überführt werden können.

Es gilt laut Aufgabenstellung Zur Überprüfung der Stabilisierbarkeit wird nun das Hurwitz-Kriterium in Abhängigkeit von auf das Nennerpolynom angewandt.

Damit (2) ein Hurwitz-Polynom ist, müssen als notwendige Bedingung alle Koeffizienten für vorhanden sein und das gleiche Vorzeichen besitzen. Die Koeffizienten sind alle vorhanden und positiv, somit muss gelten.

für

Des Weiteren gilt es die hinreichende Bedingung, dass die Hurwitzdeterminante sowie alle ihre Hauptdeterminanten müssen größer als Null sein müssen, zu überprüfen. Daraus folgt

Die beiden Hurwitz-Determinanten und det ergeben sich zu

Der geschlossene Regelkreis ist demnach für ein für das

gilt, sowie für asymptotisch stabil. Da das System durch einen P-Regler in ein HurwitzPolynom überführt werden kann, ist es mit einem P-Regler stabilisierbar.

e) Bestimmung von

Für die Aufgabe gilt . Damit ergibt sich für die Übertragungsfunktion

Die Sprungantwort des Systems berechnet sich zu . Somit lässt sich der stationäre Endwert berechnen

Damit folgt

Zwar gilt der Endwertsatz nur für stabile Systeme, jedoch kann bei der Existenz eines stationären Endwertes von der Stabiliät des Systems ausgegangen werden. Das Ergebniss kann allerdings trotzdem auf Plausibilität geprüft werden. Dies kann durch Einsetzen des erhaltenen Wertes für in das vorher berechnete Intervall für mögliche Werte von erfolgen. Das resultiert in

Der für verwendete Wert liegt in diesem Intervall, somit ist der Grenzwertsatz anwendbar und das Ergebnis plausibel.

f) Regler mit dem Verfahren nach Ziegler-Nichols auslegen

  • empirische Einstellregeln, basierend auf einem Schwingversuch
  • Regelkreis wird mit einem P-Regler geschlossen und die Regelverstärkung so lange erhöht, bis die Stabilitätsgrenze erreicht ist
  • Dafür notwendige Regelverstärkung wird mit bezeichnet, die Periodendauer der an der Stabilitätsgrenze auftretenden Dauerschwingung mit wird bezeichnet
  • Mit Hilfe dieser beiden Kennwerte lassen sich dann die Reglerparameter nach der in der Abbildung dargestellten Tabelle bestimmen

Einstellregeln nach Ziegler und Nichols

Der Stabilitätsrand wurde in Aufgabe d) bereits rechnerisch ermittelt.

P-Regler 

ergibt sich zu

ergibt sich laut Aufgabenstellung zu .

Für den P-Regler ergibt sich nach der oben dargestellten Tabelle für dessen die Übertragungsfunktion

PI-Regler 

Für den PI-Regler mit der Übertragungsfunktion

muss Reglerverstärkung zusätzlich noch die Zeitkonstante des Integrators bestimmt werden.

Aus der Tabelle ergibt sich

Die Übertragungsfunktion des PI-Reglers ergibt sich also zu

PID-Regler

Schlussendlich ergibt sich für den PID-Regler mit der Übertragungsfunktion

und dem zusätzlichen Parameter nach der Tabelle

Die Übertragungsfunktion ergibt sich damit zu

Lösung:

  2. instabil

  6. Siehe Musterlösung