8 / 15

Aufgabenstellung:

Gegeben ist das Blockschaltbild eines Nickdämpfers einer F16.

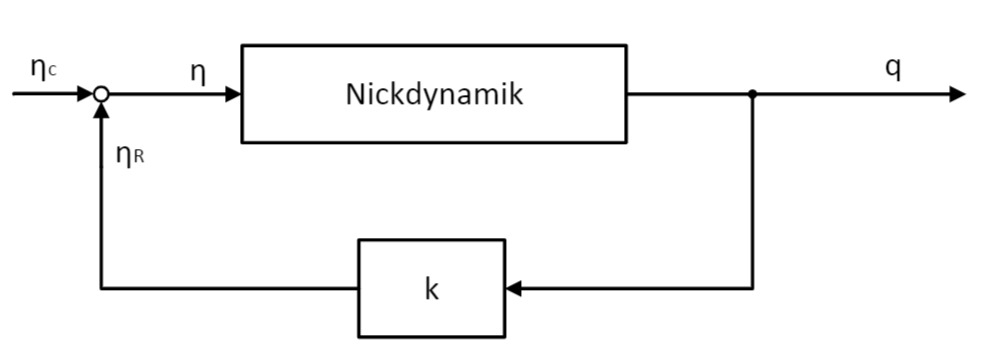
Nickdämpfer-Schaltung

Zur besseren Dämpfung einer Anstellwinkelschwingung werden Flugzeuge üblicherweise mit einem oben dargestellten Nickdämpfer versehen. Dabei wird die Nickrate über eine Verstärkung zurückgeführt und auf die von einem Piloten/Autopiloten vorgegebene Höhenruderstellung aufgeschaltet. Der Einfluss dieser Schaltung auf die Eigenschaften der Nickdynamik soll im Folgenden untersucht werden. Der erforderliche Teil der Nickdynamik einer F16 kann dabei näherungsweise mit der Übertragungsfunktion

beschrieben werden.

  1. Berechnen Sie die Pol- und Nullstellen der gegebenen Übertragungsfunktion sowie deren Eigenfrequenz und Dämpfungsgrad.

  2. Berechnen Sie nun die Eigenfrequenz und den Dämpfungsgrad des in der Aufgabe in Form eines Blockschaltbildes dargestellten Nickdämpfers in Abhängigkeit der Verstärkung .

  3. Der Verstärkungsfaktor wird auf den Wert gesetzt. Berechnen sie die Polstellen des Systems und vergleichen Sie diese sowie Frequenz und Dämpfungsgrad mit der ursprünglichen Nickdynamik.

  4. Berechnen sie den stationären Endwert beider Systeme bei einem Höhenrudersprung von und vergleichen Sie beide miteinander.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Pol- und Nullstellen sowie Eigenfrequenz und Dämpfungsgrad

Zählerpolynom:

Die Übertragungsfunktion besitzt eine Nullstelle bei .

Nennerpolynom:

Die Übertragungsfunktion besitzt ein komplexes Polstellenpaar mit negativem Realteil. Das System ist daher stabil und das Übertragungsverhalten stellt eine gedämpfte Schwingung dar.

Eigenfrequenz und Dämpfung: Koeffizientenvergleich liefert

b) Eigenfrequenz und den Dämpfungsgrad

Zunächst muss die Rückkopplung zusammengefasst werden

und damit gilt auch .

Somit folgt für die Gesamtübertragungsfunktion (positive Rückkopplung!)

Berechnung des Nenners der Gesamtübertragungsfunktion ergibt

Damit folgt für die Gesamtübertragungsfunktion

Mit Hilfe eines Koeffizientenvergleichs können dann wieder Eigenfrequenz und Dämpfung bestimmt werden

Durch die Verstärkung in der Rückführung kann also die Eigenfrequenz und Dämpfung der betrachteten Nickdynamik beeinflusst werden.

c) Polstellen und Vergleich mit der ursprünglichen Nickdynamik

Von nun an gilt , somit ergibt sich für die Polstellen der Gesamtübertragungsfunktion

Die Rückführung mit einer Verstärkung von ergibt also eine Verschiebung der Polstellen.

Mit den in b) berechneten Ausdrücken ergeben sich Eigenfrequenz und Dämpfung zu

Durch die positive Rückführung von einem wird sowohl die Eigenfrequenz als auch die Dämpfung der betrachteten Dynamik vergrößert. Da dadurch die Anstellwinkelschwingung abgeschwächt wird, spricht man bei dem vorliegenden Regelkreis in der Flugregelung von einem Nickdämpfer.

d) Stationären Endwert

Zunächst wird der Fall ohne Nickdämpfer betrachtet. Der Endwertsatz wird daher auf Sprungantwort der ursprünglichen Übertragungsfunktion aus Aufgabenstellung angewandt

Als zweites wird der Fall mit Nickdämpfer betrachtet. Anwendung des Endwertsatzes auf die Sprungantwort der Übertragungsfunktion aus Aufgabenteil b) und c) liefert

Es zeigt sich, dass durch die Rückkopplung einer Verstärkung der stationäre Endwert der Sprungantwort verkleinert wird.

Lösung:




  2.  
  3. Eigenfrequenz als auch die Dämpfung der betrachteten Dynamik wird vergrößert.