5 / 13

Aufgabenstellung:

Betrachtet wird das folgende Modell der Fahrradneigung ( Neigungswinkel, Lenkmoment):

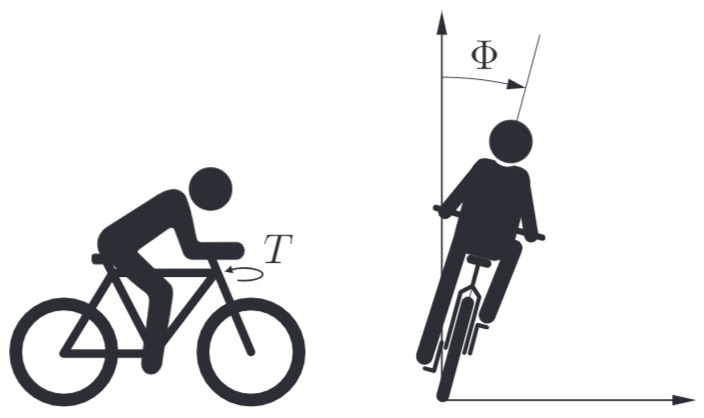
Abbildung

Die Dynamik des Fahrrads kann vereinfacht mit der folgenden Gleichung beschrieben werden ( sind konstant.):

a) Geben Sie eine linearisierte Zustandsraumdarstellung in der Form

mit für kleine Abweichungen um den Arbeitspunkt mit

an. Wählen Sie den Winkel als Ausgangsgröße.

 

Für eine bestimmte Parametrierung ergeben sich die folgenden Zustandsraummatrizen, die im Folgenden verwendet werden sollen:

b) Weisen Sie nach, dass das lineare Zustandsraummodell stabil ist.

 

Das System soll nun mit einem Zustandsregler geregelt werden.

c) Bestimmen Sie die Konstanten und so, dass der geschlossene Regelkreis die Kennkreisfrequenz und die Dämpfung aufweist.

Hinweis: Alle Aufgabenteile sind unabhängig voneinander lösbar.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Linearisierte Zustandsraumdarstellung

Zunächst wird die nichtlineare Gleichung linearisiert und der gegebene Arbeitspunkt eingesetzt:

Mit und ergibt sich das Modell im Zustandsraum zu:

b) Stabilitä nachweisen

Charakteristisches Polynom aufstellen:

Alle Koeffizienten sind vorhanden und größer als Somit sind die 1 . und 2 . Bedingung des Stabilitätskriteriums nach Hurwitz erfüllt. Das System ist stabil!

c) Konstanten und

Der Skalar der Eingangsgrößsen wird in das Zustandsraummodell eingesetzt, sodass sich die neue Systemmatrix ergibt:

Bestimmung des charakteristischen Polynoms von :

Das Sollpolynom eines schwingungsfähigen -Elements aufstellen:

Mithilfe eines Koeffizientenvergleichs können die Parameter nun bestimmt werden:


Lösung:



  2. stabil

  3. ;