4 / 13

Aufgabenstellung:

Eine Magnetschwebebahn soll elektrodynamisch zum Schweben gebracht werden, was eine aktive Abstandsregelung erfordert.

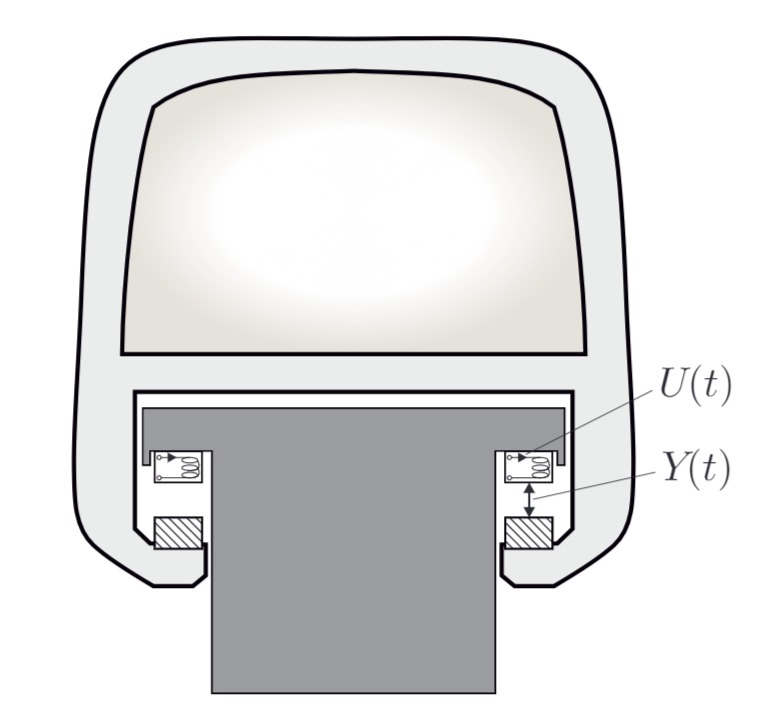
Abbildung

Luftspaltbreite (Regelgröße)

Spulenstrom (Eingangsgröße)


Das betrachtete System wird durch folgende nichtlineare Differentialgleichung beschrieben:

mit

a) Definieren Sie geeignete Zustandsgrößen und bestimmen Sie eine äquivalente Beschreibung des Systems durch einen Satz von Differentialgleichungen 1. Ordnung.

b) Bestimmen Sie , sodass sich im stationären Fall am Ausgang einstellt.

c) Linearisieren Sie das System um den Arbeitspunkt . Kennzeichnen Sie die Matrizen und der linearen Zustandsraumdarstellung explizit.

 

Hinweis: Die folgenden Aufgabenteile sind unabhängig von den vorherigen lösbar.

 

Im Folgenden soll nur noch das linearisierte Streckenmodell verwendet werden, für das mit einer bestimmten Parametrierung gilt:

d) Ist das System stabil? Ist es steuerbar?

Für das System soll nun ein Zustandsregler mit mit Polvorgabe entworfen werden, sodass der geschlossene Regelkreis nicht schwingungsfähig ist und alle Zeitkonstanten 0,5 sec betragen.

e) Berechnen Sie die Rückführmatrix der Zustandsrückführung.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Zustandsgrößen und Differentialgleichungen 1.Ordnung

Die gegebene Differentialgleichung beschreibt ein System zweiter Ordnung. Ein geeigneter Zustandsvektor lautet:

Anhand des eingeführten Zustandsvektors kann die Prozessbeschreibung in ein System von (nichtlinearen) Differentialgleichungen erster Ordnung überführt werden

mit

b) im Stationären Fall

Für Ruhelagen des Systems bzw. Stationarität gilt:

0.

Somit ergeben sich zwei Bedingungen

Mit sowie der Nebenbedingung folgt schlieflich

c) Linearisieren um den Arbeitspunkt

Durch die Linearisierung des Systems um die Ruhelage verschwindet der erste Term der Taylorreihenentwicklung.

Ausgewertet am Linearisierungspunkt berechnen sich die Jacobi-Matrizen zu:

d) Stabilität und Steuerbarkeit

Berechnung des charakteristischen Polynoms:

Da im charakteristischen Polynom der Koeffizient des Terms erster Ordnung fehlt, folgt nach dem Hurwitz-Kriterium die Instabilität des ungeregelten Systems.

Berechnung der Steuerbarkeitsmatrix :

Es gilt . Das linearisierte System ist daher steuerbar.

e) Rückführmatrix

Für den durch Zustandsrückführung geschlossenen Regelkreis sind entsprechend der Systemordnung zwei Pole vorzugeben. Wegen der Forderung 0,5 sec wird für den geschlossenen Regelkreis ein doppelter reeller Eigenwert bei gefordert.

Das Wunschpolynom lautet somit

Sei die zu bestimmende Rückführmatrix, dann folgt für die Systemmatrix des Übertragungssystems mit Rückführung:

Das charakteristische Polynom des geschlossenen Regelkreises berechnet sich somit zu

Koeffizientenvergleich zwischen Wunschpolynom und charakteristischem Polynom des Regelkreises liefert

Es ergibt sich die Verstärkung der Zustandsrückführung zu .

Lösung:



  1.  



  4. instabil und steuerbar