6 / 13

Aufgabenstellung:

Betrachtet wird ein inverses Pendel mit geschwindigkeitsabhängiger Lagerreibung gemäß folgender Abbildung:

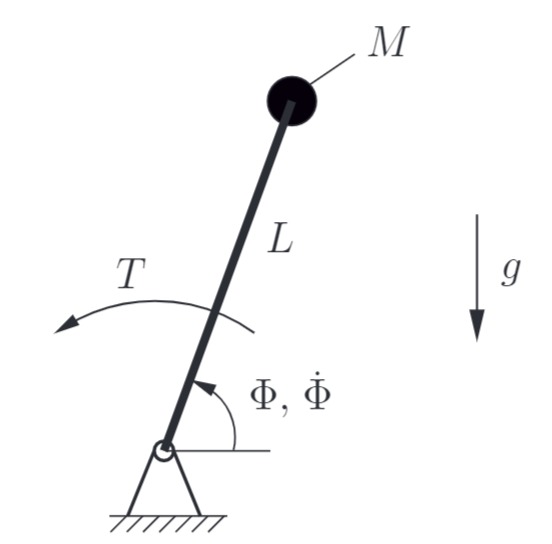
Abbildung

Winkel

Winkelgeschwindigkeit

Motormoment

Pendellänge

Punktmasse am Ende des Pendels

Erdbeschleunigung

Das System kann durch folgende nichtlineare Differentialgleichung im Bereich beschrieben werden:

Der Winkel soll mit Hilfe des Motormoments in der oberen Ruhelage eingeregelt werden. und sind konstant.


Hinweis: Die Aufgabenteile a), b) und c)-d) können unabhängig voneinander gelöst werden.

a) Geben Sie eine linearisierte Zustandsraumdarstellung der Regelstrecke in der Form

mit für kleine Abweichungen um den Arbeitspunkt an.


Für eine bestimmte Parametrierung ergeben sich die folgenden Zustandsraummatrizen, die im Folgenden verwendet werden sollen:

b) Ist dieses System steuerbar?

Es soll ein Zustandsregler mit der Rückführung ausgelegt werden.

c) Geben Sie die neue Systemmatrix für den geschlossenen Regelkreis in Abhängigkeit von und an.
d) Bestimmen Sie die Stabilitätsbedingungen für und , sodass der geschlossene Regelkreis BIBO-stabil ist. Zeichnen Sie die Stabilitätsgrenzen in das folgende Diagramm ein und schraffieren Sie die stabilen Bereiche.

Abbildung

 

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) linearisierte Zustandsraumdarstellung

Umstellen der Gleichung nach und anschließende Linearisierung der gegebenen Gleichung für kleine Abweichungen ergibt:

Einsetzen des gegebenen Arbeitspunktes :

Mit und (der Winkel soll mithilfe des Motormoments geregelt werden) ergibt sich das Modell im Zustandsraum zu:

b) Steuerbarkeit

Steuerbarkeitsmatrix aufstellen:

besitzt vollen Rang . Damit ist das System steuerbar.

c) Systemmatrix

Einsetzen von in das gegebene linearisierte Gleichungssystem ergibt direkt die neue Matrix :

d) Stabilitätsbedingungen für und

Notwendige und hinreichende Bedingung für die Stabilität des geschlossenen Regelkreises: Alle Eigenwerte von müssen negative Realteile besitzen.

Charakteristisches Polynom:

Damit alle Eigenwerte negativen Realteil haben, müssen alle Koeffizienten vorhanden und positiv sein. Daraus ergeben sich 2 Bedingungen an und

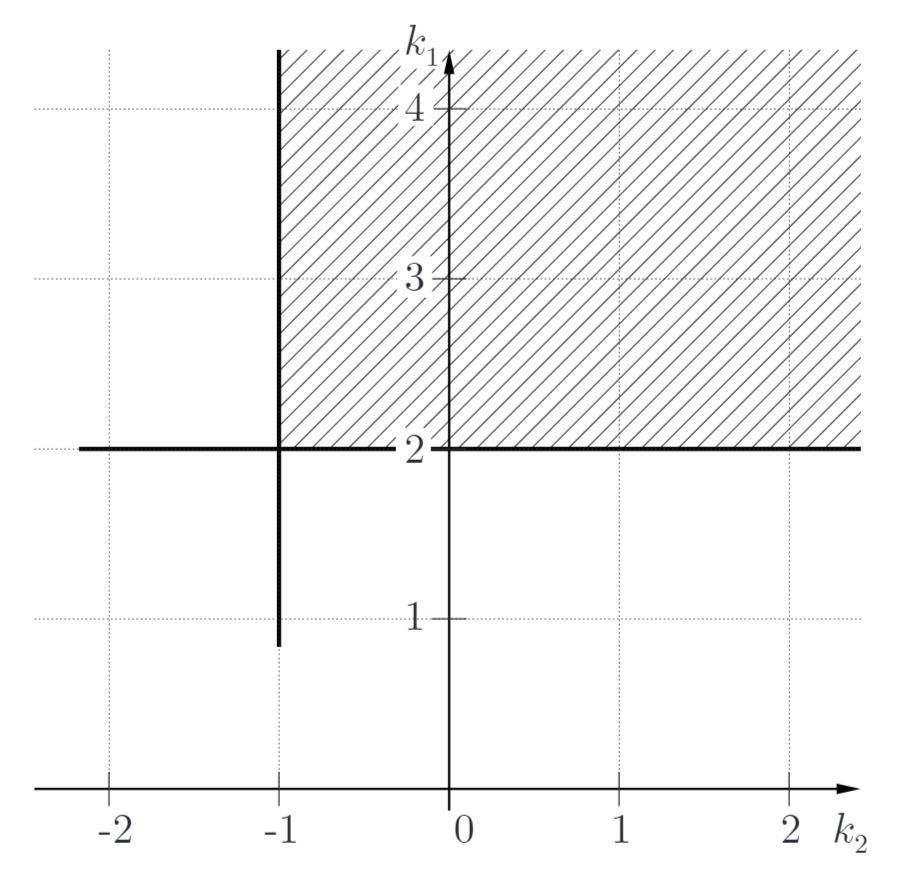
Abbildung

Lösung:

  2. steuerbar

  4. ;