Aufgabenstellung:
Für die Regelstrecke aus der ersten Aufgabe sollen nun auch die Parameter
- Die Durchtrittsfrequenz
der Kreisverstärkung soll bei liegen. - Die Nyquistkurve der Kreisverstärkung soll den Einheitskreis tangential zur imaginären Achse betreten.
- Es soll kein stationärer Regelfehler auftreten.
Gehen Sie für den Reglerentwurf wie folgt vor:
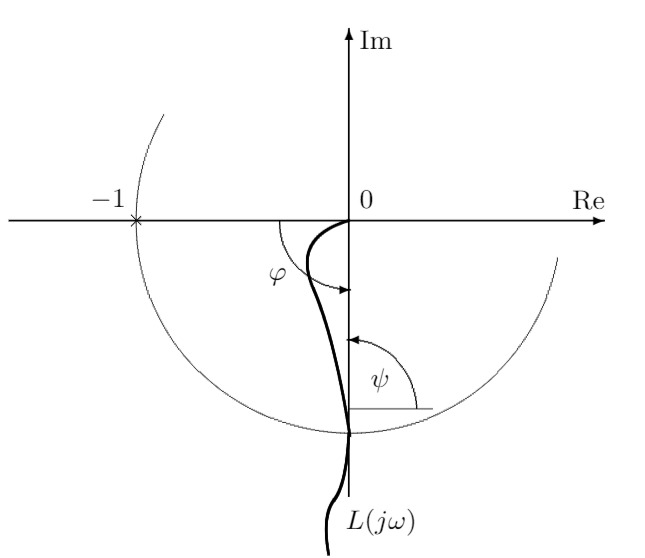
a) Bestimmen Sie aufgrund geometrischer Überlegungen die Phasenreserve
b) Leiten Sie die analytischen Ausdrücke für die Grössen
Lösungsweg:
a) Phasenreserve
Die Phasenreserve
Um einen verschwindenden stationären Nachlauffehler zu erhalten, muss der Betrag der Kreisverstärkung für
Die Nyquist-Kurve der Strecke
b) analytischen Ausdrücke für die Grössen
Der analytische Ausdruck für den Betrag der Strecke lautet:
Bei der Durchtrittsfrequenz
Die Ableitung des Betrags nach der Frequenz
Ausgewertet an der Durchtrittsfrequenz
Für die Phase der Strecke gilt:
Bei der Durchtrittsfrequenz hat die Strecke demnach die Phase
Die Ableitung der Phase nach
Ausgewertet an der Durchtrittsfrequenz
Lösung:
-