3 / 3

Aufgabenstellung:

Gegeben Sei die Regelstrecke:

Entwerfen Sie einen prädiktiven Regler, so dass die Zeitkonstante des resultierenden Regelsystems zwei mal kleiner ist als jene der Regelstrecke. Gehen Sie dabei wie folgt vor:

  1. Skizzieren Sie qualitativ den Frequenzgang der Regelstrecke in einem Nyquist Diagramm.
  2. Geben Sie die Übertragungsfunktion des spezifizierten Regelsystems (Referenzsystem) an.
  3. Zeichnen Sie das Signalflussbild des Regelsystems.
  4. Leiten Sie den internen Regler als Funktion des Referenzsystems her, zuerst allgemein und dann für die gegebene Regelstrecke. Um was für einen Regler handelt es sich?

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Skizzieren des Frequenzgangs 

Das Nyquist-Diagramm der Regelstrecke sieht folgendermassen aus

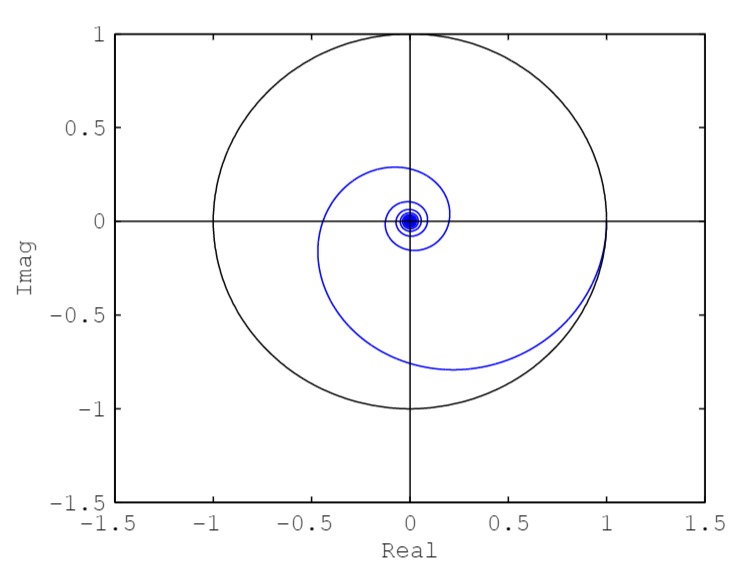
Abbildung

b) Übertragungsfunktion

Das Referenzsystem soll eine Zeitkonstante aufweisen die halb so gross ist wie die der Regelstrecke. Die Totzeit kann durch die Regelung nicht kompensiert werden, daher muss das Referenzsystem die gleiche Totzeit aufweisen, wie die Strecke.

c) Signalflussbild des Regelsystems

Die Abbildung zeigt das Signalflussbild des prädiktiven Reglers

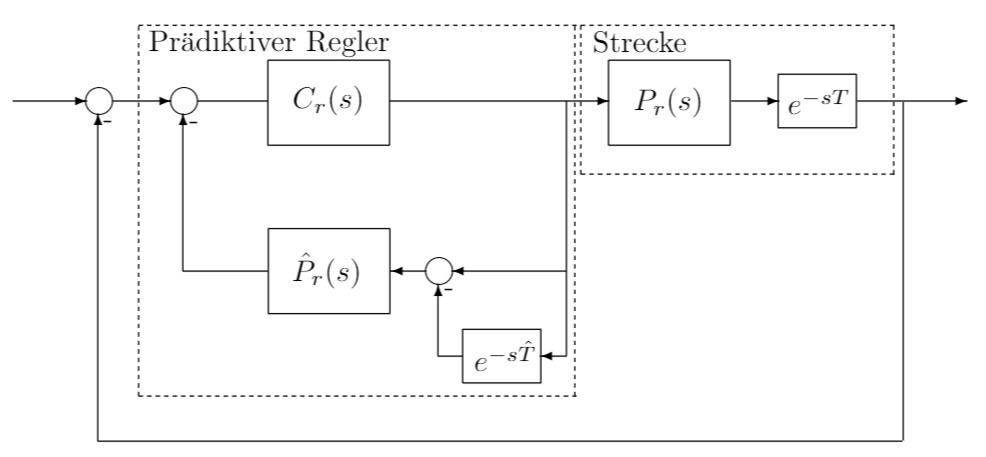
Abbildung

d) interner Regler  

Es wird nun angenommen, dass das Strecke perfekt modelliert ist d.h. und . Die Übertragungsfunktion des gesamten Reglers wird somit

Die Übertragungsfunktion des Regelsystems wird somit

Vergleicht man diese nun mit dem Referenzsystem , also und löst nach auf, ergibt das

Setzt man die Strecke aus der Aufgabe ein erhält man:

Also einen PI-Regler mit und .

Lösung:

  1. siehe Musterlösung
  3. siehe Musterlösung
  4. , PI-Regler mit und