1 / 3

Aufgabenstellung:

Für die Regelstrecke mit der Übertragungsfunktion

sollen die Parameter und eines PID-Reglers gemäss den Regeln von Aström-Hägglund bestimmt werden.
Gehen Sie für den Reglerentwurf wie folgt vor:

  1. Skizzieren Sie den qualitativen Verlauf der Regelstrecke in einem Nyquist-Diagramm und berechnen Sie den statischen Übertragungsfaktor .
  2. Bestimmen Sie die kritische Verstärkung und die zugehörige Periode .
  3. Berechnen Sie die Parameter und des PID-Reglers gemäß dem Schema von Aström-Hägglund für

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) qualitativen Verlauf der Regelstrecke und statischer Übertragungsfaktor

Die folgende Abbildung zeigt das Nyquist-Diagramm der Strecke.

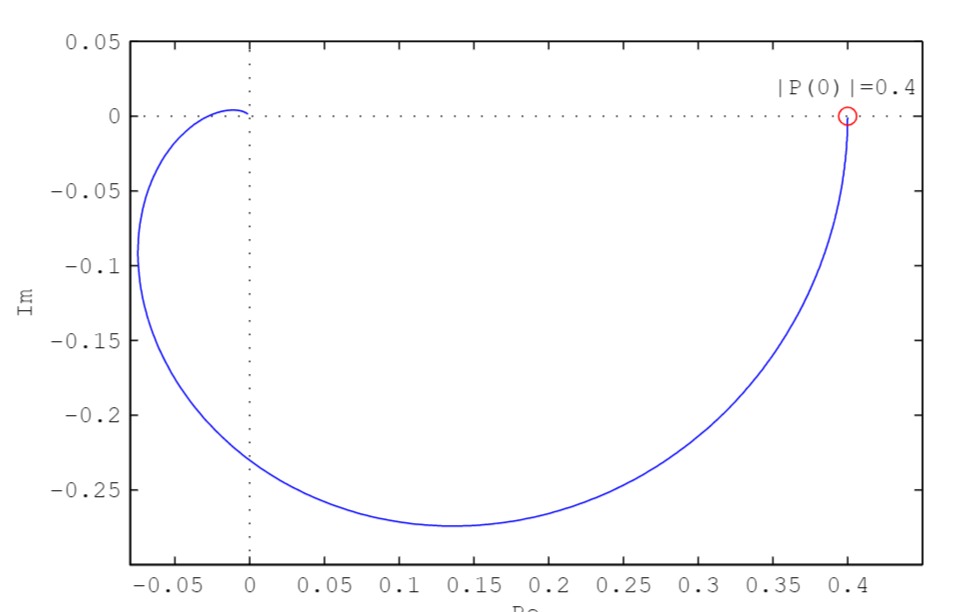
Abbildung

Der DC-Gain der Strecke beträgt

b) Verstärkung und die zugehörige Periode

Für den Frequenzgang der Strecke gilt:

Der analytische Ausdruck für den Betrag der Strecke lautet demnach:

Man kann für die Phase der Strecke direkt den folgenden Ausdruck herleiten:

Für die Berechnung der kritischen Verstärkung interessiert der Betrag der Strecke bei einer Phase von . Es gilt (Vergleiche mit obiger Abbildung):

wobei

Es lässt sich die Frequenz bestimmen.

Die kritische Verstärkung folgt zu

Für die Periode gilt:

Bemerkung: Anstatt via Phase und Betrag können die kritischen Werte und auch über den Imaginär- und den Realteil von bestimmt werden.

Es gilt:

Der imaginäre und der reale Teil werden getrennt und die zwei erhaltenen Gleichungen gelöst.

c) und  

Für und einen PID-Regler lauten die zu nutzenden Werte für und zur Berechnung für die Aström-Hägglund Parameter wie folgt:

Mit dem Parameter

Nun lassen sich die gesuchten Reglerparameter berechnen:

Lösung:

  1. siehe Musterlösung;

  2. ,