2 / 9

Aufgabenstellung:

  1. Geben Sie die allgemeine Differentialgleichung und die Übertragungsfunktion für ein Glied an.
    Gegeben sind jetzt die Parameter und die Zeitkonstante
  2. Zeichnen Sie hierfür in das folgende Bild den Verlauf der Ausgangsgröße für die dargestellte sprungförmige Änderung der Eingangsgröße mit allen relevanten Angaben ein.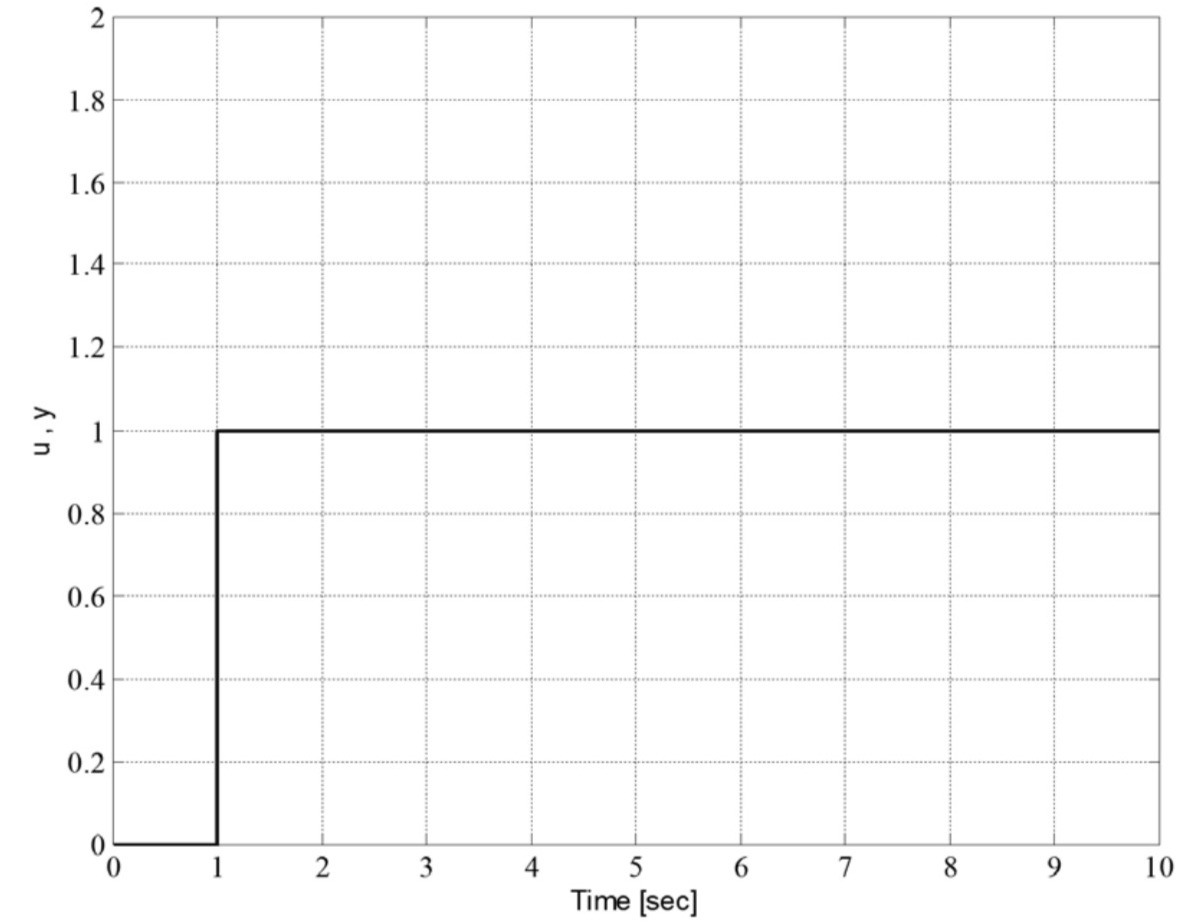
    Sprungantwort eines DT1_Glieds

  3. Geben Sie den Frequenzgang des -Glieds an.

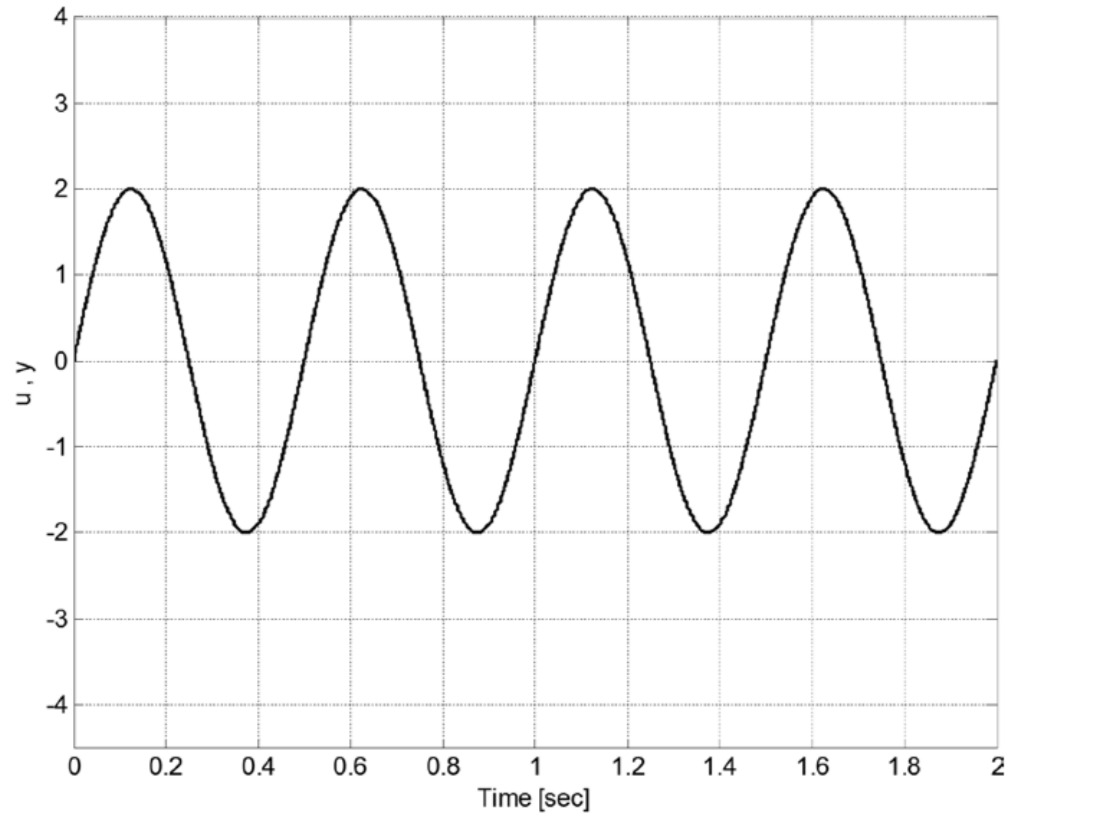
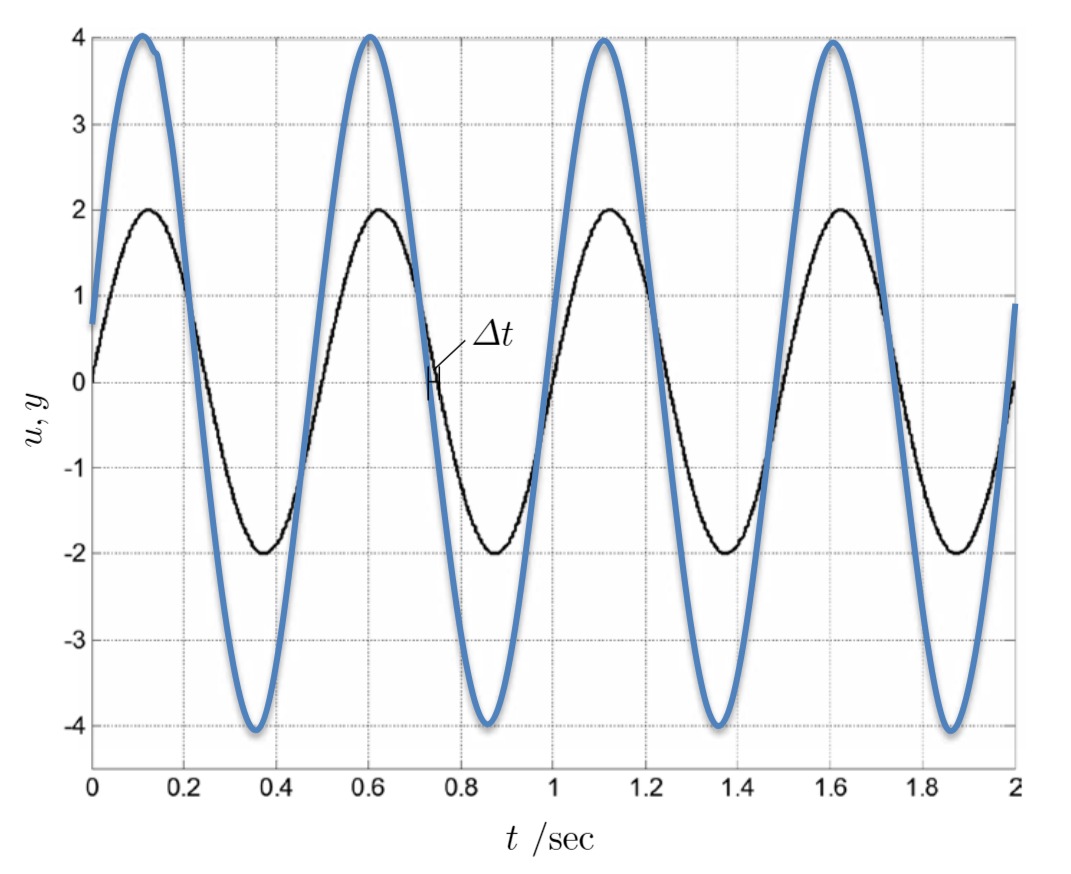
  4. Weiterhin ist in Bild der Verlauf einer sinusförmigen Eingangsgröße dargestellt. Skizzieren Sie hier den Verlauf der zugehörigen Ausgangsgröße (eingeschwungener Zustand) für dieses Übertragungsglied.
    Hinweise:

    • Amplitude und Frequenz von ermitteln

    • Amplitude und Phasenverschiebung berechnen

    • Lage der Nulldurchgänge und Maxima/Minima einzeichnen

    • Verlauf frei Hand einzeichnen

     Abbildung

  5. Zeichnen Sie den Amplituden- und Phasengang im folgenden Bode-Diagramm ein.

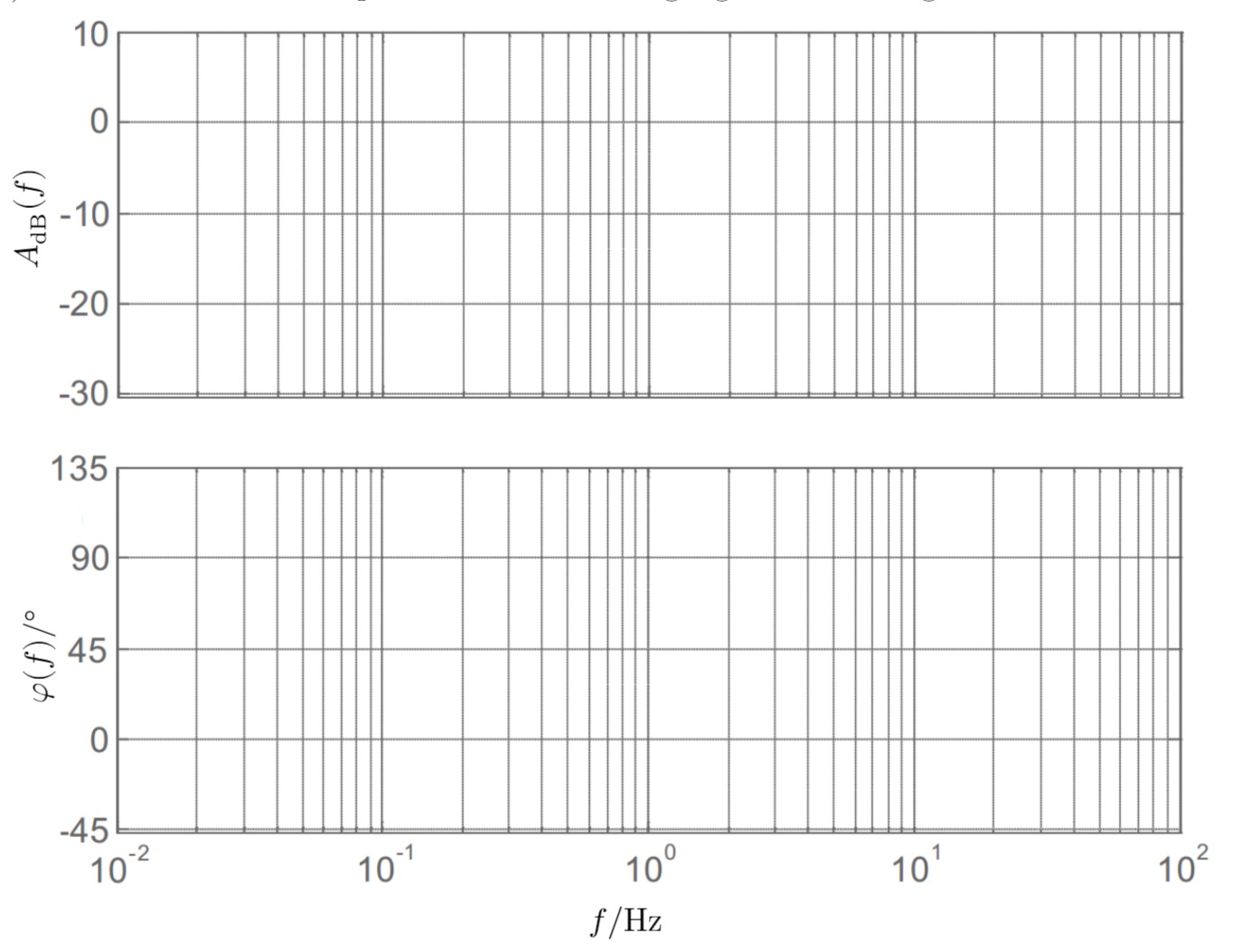
    Abbildung

     

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Allgemeine Differentialgleichung und Übertragungsglied

b) Verlauf der Ausgangsgröße zeichnen

Bestimmen der notwendigen Parameter (Formelsammlung):

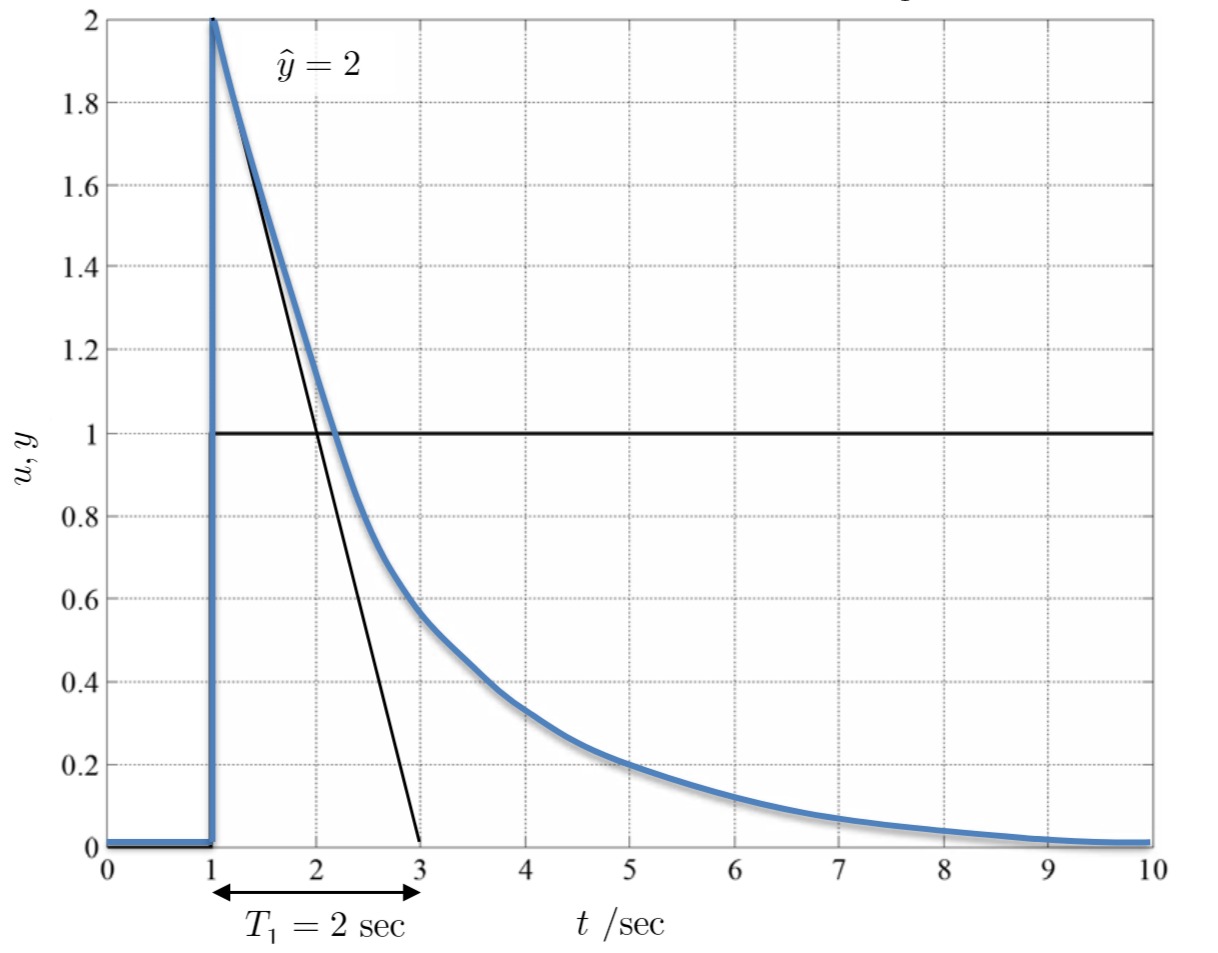
Abbildung

c) Frequenzgang des -Glieds

Berechnen der Amplitude und Phase für

Verstärkung der Amplitude um den Faktor 2.

Positive Phasenverschiebung, d.h. Voreilung des Ausgangssignals.

d) Verlauf der Ausgangsgröße

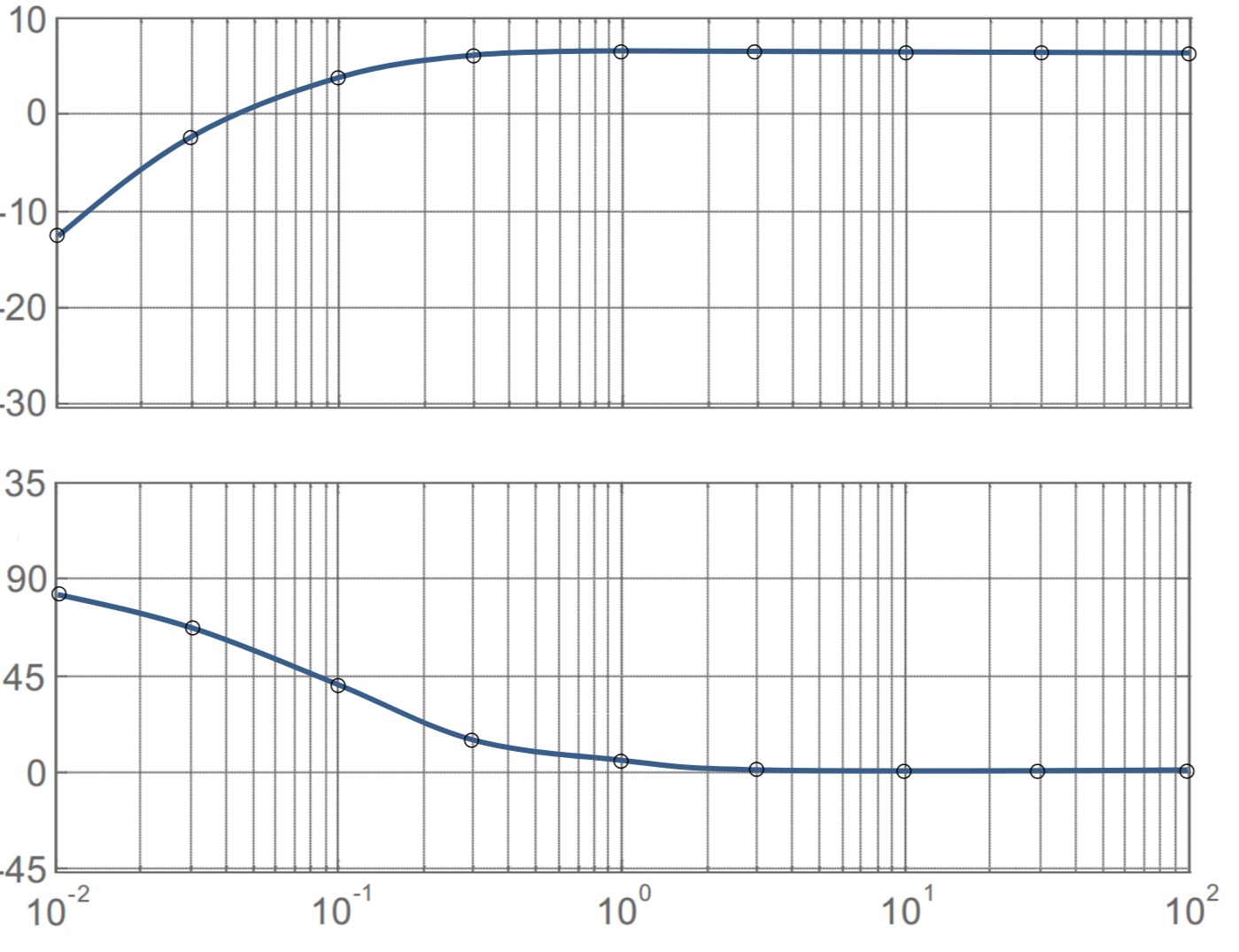
Abbildung

e) Amplituden- und Phasengang zeichnen

Amplitudengang und Phase in Abhängigkeit von fotmulieren und Wertetabelle anlegen:

Abbildung

Lösung:


  2. Siehe Musterlösung.


  4. Siehe Musterlösung.
  5. Siehe Musterlösung.