Aufgabenstellung:
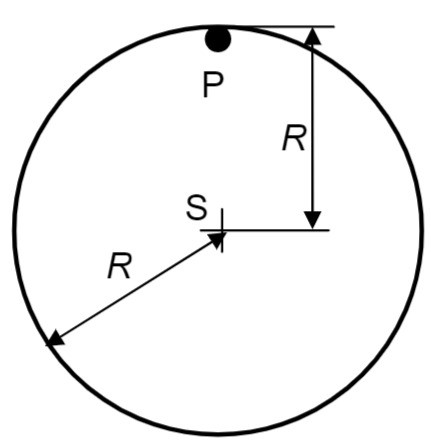
Ein Reifen - ein sehr dünnwandiger Kreisring - hat einen Durchmesser
Der Reifen wird über einen horizontal in die Wand getriebenen Nagel gehängt.
-
Geben Sie die Schwingungsdauer
und die Frequenz des schwingenden Reifens bei kleinen Auslenkungen des Reifens aus der Ruhelage an. -
Bestimmen Sie die Länge
eines mathematischen Pendels, das die gleiche Schwingungsdauer wie der Reifen hat.
Lösungsweg:
Vorbemerkung:
- Für einen Reifen gilt: Wandstärke
Durchmesser; dies ist wichtig für die Bestimmung des Massenträgheitsmoments. - Die Beschränkung auf kleine Auslenkungen ist notwendig für die Linearisierung der Differentialgleichung.
Es werden folgende Bezeichnungen gewählt:
Massenträgheitsmoment des Körpers (Reifen)
bezüglich einer Drehachse durch PMassenträgheitsmoment des Körpers (Reifen) bezüglich einer Achse durch den Massenmittelpunkt (Achsen durch und parallel) Abstand Drehachse durch Aufhängepunkt - Massenmittelpunkt Für die gegebene Geometrie ist Gesamtmasse des Reifens Fallbeschleunigung nahe der Erdoberfläche
a) Schwingungsdauer
Für die Schwingungsdauer eines physikalischen Pendels gilt bei kleinen Auslenkungen aus der Ruhelage (notwendig zur Linearisierung der Differentialgleichung)
Das Massenträgheitsmoment
Einsetzen von
Die Schwingungsdauer bei kleinen Auslenkungen aus der Ruhelage wird damit
Die Schwingungsdauer
Die Schwingungsdauer ergibt sich zu
Die Eigenfrequenz der Schwingungen ist damit:
b) Bestimmen Sie die Länge
Die Schwingungsdauer eines mathematischen Pendels ist
Die Schwingungsdauer des Reifens (physikalisches Pendel) ist
Diese beiden Schwingungsdauern sollen gleich sein. Also muss gelten
Vergleich der Radikanden liefert als Länge
Anmerkung
Man nennt die Länge dieses, der Schwingungsdauer des physikalischen Pendels äquivalenten mathematischen Pendels, die reduzierte Pendellänge
Lösung:
-
Schwingungsdauer
(unabhängig von Reifenmasse).
Eigenfrequenz. -
Länge
.