Schwingungen - Freie, harmonische Schwingungen

11 / 18

Aufgabenstellung:

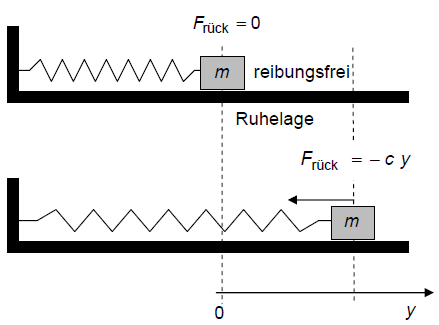
new alt text

Bei der Bestimmung der Federkonstanten einer Schraubenfeder misst man für eine wirkende äußere Kraft eine Verlängerung der Feder um .

Nach Bestimmung der Federkonstanten wird, in horizontaler Anordnung; (vgl. Abbildung) ein Körper (Masse ) am Ende der Feder befestigt und aus der Ruhelage der Feder um auf einer ideal reibungsfreien Unterlage ausgelenkt. Danach wird der Körper ohne Anfangsgeschwindigkeit losgelassen.
Der Körper führt anschließend ungedämpfte harmonische Schwingungen aus.

Welche Federkonstante hat die Feder?
Welchen Betrag hat die Kraft, den die Feder auf den Körper zum Zeitpunkt ausübt, in welchem er losgelassen wird?
Geben Sie die Schwingungsdauer , die Eigenfrequenz und die Eigenkreisfrequenz des Feder-Masse-Systems an.
Bestimmen Sie die Amplitude und den Nullphasenwinkel der ungedämpften harmonischen Schwingung.
Geben Sie das Weg-Zeit-Gesetz für die Bewegung dieses Systems an.
Welche Maximalgeschwindigkeit hat der schwingende Körper?
Welche Maximalbeschleunigung hat der schwingende Körper?
Berechnen Sie die Geschwindigkeit, die Beschleunigung, die kinetische und potentielle Energie für den Punkt der Bahnkurve, der gerade in der Mitte von Anfangslage und Gleichgewichtslage liegt.
Welche Gesamtenergie hat das Feder-Masse-System?

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Bestimmung der Federkonstanten

Vorbemerkung: Es liegt ein eindimensionales Problem vor. Man legt ein Koordinatensystem durch Wahl einer positiven -Richtung zweckmäßigerweise so fest, dass die Verlängerung der Feder parallel zu dieser Achse erfolgt und die Gleichgewichtslage der Feder markiert. Anstelle mit den vektoriellen Größen kann dann einfach mit den Koordinaten oder Beträgen gerechnet werden. Ein negativer Wert für eine physikalische Größe bedeutet, dass der zugehörige Vektor in Richtung negativer Werte der -Achse gerichtet ist.

Das Kraftgesetz für eine ideale Feder lautet

$ü$

Da die Federkonstante positiv ist, bedeutet das Minuszeichen, dass bei Auslenkung der Feder in positiver (negativer) -Richtung die rücktreibende Kraft in die negative (positive) -Richtung gerichtet ist. Die äußere Kraft muss der rücktreibenden Kraft der Feder stets das Gleichgewicht halten;

Also gilt für :

$ü$

b) Welchen Betrag hat die Kraft, den die Feder auf den Körper zum Zeitpunkt ausübt, in welchem er losgelassen wird?

Rückstellkraft bei Auslenken der Feder um

$ü$

Diese rücktreibende Kraft hängt nur von der Auslenkung der Feder ab, sie ist unabhängig von der Masse des angehängten Körpers.

c) Geben Sie die Schwingungsdauer , die Eigenfrequenz und die Eigenkreisfrequenz des Feder-Masse-Systems an.

Die Schwingungsdauer des Feder-Masse-Systems bestimmt sich aus

Die Eigenfrequenz ergibt sich zu

Die Eigenkreisfrequenz wird

d) Bestimmen Sie die Amplitude und den Nullphasenwinkel der ungedämpften harmonischen Schwingung.

Das Weg-Zeit-Gesetz einer ungedämpften harmonischen Schwingung lautet allgemein

Das Geschwindigkeit-Zeit-Gesetz ist die erste Ableitung des Weg-Zeit-Gesetzes

Die Integrationskonstanten und können mit Hilfe der Anfangsbedingungen für Auslenkung und Geschwindigkeit berechnet werden.

Der Körper wird zum Zeitpunkt s nach Auslenken aus der Ruhelage ohne Anfangsgeschwindigkeit losgelassen.

Einsetzen dieser speziellen Anfangsbedingungen liefert zwei Gleichungen für die beiden Unbekannten und

Weg-Zeit-Gesetz für

Geschwindigkeit-Zeit-Gesetz für

Wenn ein Produkt aus drei Größen null sein soll, dann muss mindestens einer der Multiplikatoren null sein. Da weder die Amplitude noch die Eigenkreisfrequenz null sind, folgt aus der zweiten Gleichung notwendigerweise

Damit wird der Nullphasenwinkel

Diesen Nullphasenwinkel eingesetzt in die erste Gleichung ergibt die Amplitude

e) Geben Sie das Weg-Zeit-Gesetz für die Bewegung dieses Systems an

Die Bewegungsgleichung des Körpers bei den gegebenen Anfangsbedingungen wird damit durch das folgende Weg-Zeit-Gesetz beschrieben

f) Welche Maximalgeschwindigkeit hat der schwingende Körper?

Die Geschwindigkeit ist allgemein durch das Geschwindigkeit-Zeit-Gesetz als erste Ableitung des Weg-Zeit-Gesetzes gegeben

Da gilt, wird der Betrag der Maximalgeschwindigkeit bestimmt durch den Vorfaktor der Sinus-Funktion; also

Dieser Wert wird betragsmäßig in einer Schwingungsperiode zweimal erreicht und zwar jeweils beim Durchgang durch die Ruhelage (in zwei verschiedene Bewegungs-Richtungen).

g) Welche Maximalbeschleunigung hat der schwingende Körper?

Die Beschleunigung erhält man allgemein durch Ableiten der Geschwindigkeit nach der Zeit ; also

Damit gilt der Betrag der Maximalbeschleunigung, wieder als Vorfaktor der Kosinus-Funktion

Diese maximale Beschleunigung (und die zur Beschleunigung proportionale Kraft) tritt in den beiden Umkehrpunkten auf.

h) Berechnen Sie die Geschwindigkeit, die Beschleunigung, die kinetische und potentielle Energie für den Punkt der Bahnkurve, der gerade in der Mitte von Anfangslage und Gleichgewichtslage liegt.

Für den Bahnpunkt in der Mitte zwischen Ausgangs- und Gleichgewichtslage ist die Auslenkung aus der Ruhelage

Zunächst wird berechnet, nach welcher Zeit dieser Bahnpunkt erreicht wird.

Daraus folgt für das Argument des Kosinus:

und damit gilt für die Zeit:

Diese Zeit braucht man aber zahlenmäßig für weitere Rechnungen nicht, es tritt in den harmonischen Funktionen jeweils nur der Ausdruck als Phasenwinkel (Argument) der harmonischen Funktionen auf.

Am Ort wird die Geschwindigkeit

und die Beschleunigung

Energieanteile

Die potentielle Energie einer (idealen) Feder ist gegeben durch

Für wird diese zu

Für erhält man mit

i) Welche Gesamtenergie hat das Feder-Masse-System?

Die Gesamtenergie ist gegeben durch

Mit den Werten von Aufgabenteil (h) ergibt sich

Probe

Für die Gesamtenergie eines idealen Feder-Masse-System gilt allgemein

Dies liefert mit den Werten wie erwartet das gleiche Ergebnis

Lösung:

Federkonstante .
Rückstellkraft für .
Schwingungsdauer

Eigenfrequenz .
Eigenkreisfrequenz .
Nullphasenwinkel und Amplitude .
Weg-Zeit-Gesetz .
Maximalgeschwindigkeit .
Maximalbeschleunigung .
Geschwindigkeit .
Beschleunigung .
Potentielle Energie .
Kinetische Energie .
Gesamtenergie