Aufgabenstellung:
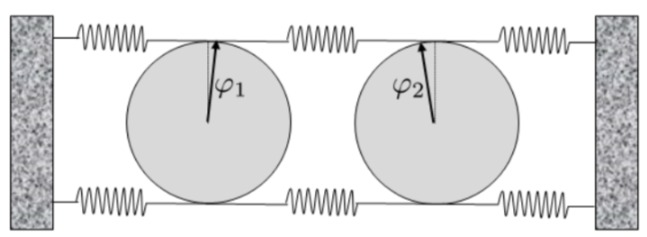
Zwei Drehscheiben (Masse
- Welche Drehmomente
und wirken auf die beiden Scheiben? - Führen Sie die Koordinaten
und ein. Wie lauten damit die Bewegungsgleichungen für das System für die gleichphasige Schwingung und für die gegenphasige Schwingung - Welche Frequenzen
und haben die gleich- bzw. gegenphasige Schwingung? - Nun seinen die Zahlenwerte
und gegeben, Berechnen Sie die Periodendauer der gegenphasigen Schwingung.
Hinweis: Trägheitsmoment einer Scheibe bzgl. der Symmetrieachse
Lösungsweg:
Für kleine Winkel

a) Drehmomente
Drehmomente ergeben sich aus den Kräften, die die Federn auf die Scheiben ausrichten. Der Angriffspunkt ist jeweils
b) Bewegungsgleichungen
Für die Bewegungsgleichungen wird verwendet, dass
Daraus folgen die Bewegungsgleichungen für
Diese beiden Bewegungsgleichungen sind offensichtlich gekoppelt. Um die beiden Gleichungen zu entkoppeln werden neue Variablen wie in der Angabe eingeführt
Die Bewegungsgleichungen für diese Variablen folgen aus Summe bzw. Differenz der Gleichungen für
Für gleichphasige Schwingung gilt, dass
Analog folgt für die gegenphasige Schwingung
c) Schwingungsfrequenzen
Die Schwingungsfrequenzen können leicht aus den jeweiligen Bewegungsgleichungen abgelesen werden
d) Für die Schwingungsperiode folgt