Aufgabenstellung:
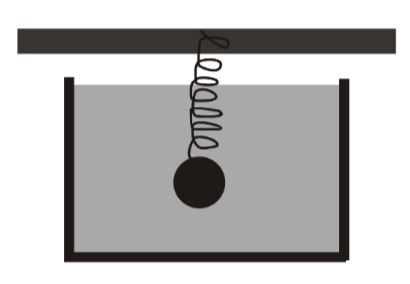
Eine Kugel mit Radius
- Berechnen Sie die Gesamtkraft und bestimmen Sie daraus die Differentialgleichung (DGL) für die Beschleunigung der Kugel. Verwende
und . - Verwenden Sie für die Lösung der homogenen DGL folgenden Ansatz:
. Bestimmen Sie die Konstante und daraus die Lösung, die für den Fall gilt.
Hinweis: Durch Verwendung der Euler'schen Formel kannauch in der Form geschrieben werden, und sind beliebige reelle Zahlen. - Für eine Lösung der inhomogenen Differentialgleichung soll eine konstante Funktion angenommen werden. Wie lautet nun die gesamte Lösung der DGL?
- Nehmen Sie nun
(inhomogener Teil der DGL fällt dadurch weg) an und bestimme die Konstanten durch die Anfangsbedingungen und
Lösungsweg:
a) Gesamtkraft und DGL
Auf die Kugel wirkt die Gewichtskraft, die Auftriebkraft, die Federkraft und die Reibung durch die Flüssigkeit
Dies kann zur üblichen Form der Differentialgleichung für
wobei
b) Konstante
Der homogene Teil der DGL lautet
Einsetzten des Ansatzes aus der Angabe liefert die Bestimmungsgleichung für die Konstante
Es ergeben sich drei mögliche Fälle:
1.
Der Term unter der Wurzel ist positiv, somit ist die Wurzel reell und
2.
Die Wurzel fällt weg. Es gibt nur eine Lösung, ein exponentieller Abfall
3.
Der Term unter der Wurzel ist negativ, die Wurzel wird rein imaginär und
wobei
c) Gesamtlösung der DGL:
Um den inhomogenen Teil der DGL zu lösen wird der Ansatz der rechten Seite verwendet. Da die Inhomogenität konstant ist wird als Ansatz eine Konstante gewählt
Einsetzten in die DGL liefert
Es folgt für C:
Die gesamte Lösung der DGL setzt sich als Summe der homogenen und der partikulär Lösung zusammen.
d) Bestimmung der Konstanten:
Im Folgenden wird angenommen, dass