Aufgabenstellung:
Ein dünner ausbalancierter Waagebalken mit Masse
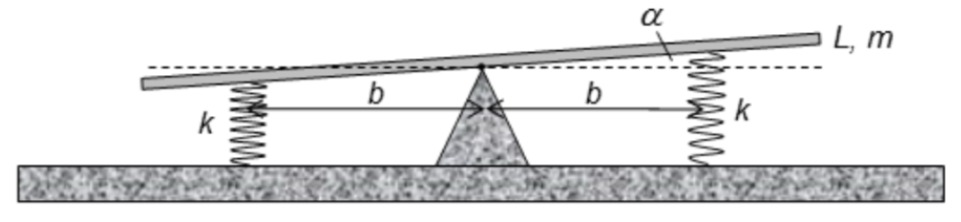
- Welches Rückstellende Drehmoment
wirkt, wenn der Balken um einen kleinen Winkel gekippt wird? Geben Sie einen Näherungsausdruck an, der linear in ist. - Wie hängt die Winkelbeschleunigung
mit dem kleinen Winkel zusammen? - Welche Schwingungsperiode
hat die Kippschwingung des Balkens? - Für die Anordnung seien Zahlenwerte
und gegeben. Für die Schwingungsperiode werde s gemessen. Was ergibt sich hieraus für die Federkonstante
Lösungsweg:
a) Rückstellendes Drehmoment
Wenn der Balken um einen kleinen Winkel
b)
Um die Winkelbeschleunigung
Aus
c) Winkelbeschleunigung
Wird die Bewegungsgleichung in der Form
d) Federkonstante
Umformen der Schwingungsperiode nach