Aufgabenstellung:
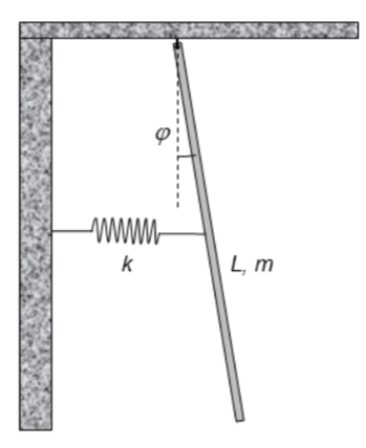
Eine dünne Stange (Masse
- Welches gesamte Drehmoment
wirkt auf dieses Stangenpendel, wenn es um einen kleinen Winkel ausgelenkt wird? (nur 1. Ordnung von ) - Stellen Sie die Bewegungsgleichung auf.
- Mit welcher Frequenz schwingt das Pendel?
- Stellen Sie das Ergebnis in dimensionslos dar, indem sie
angeben, wobei die Frequenz für ist. Geben Sie einen Näherungsausdruck an, der dann gültig ist, wenn eine kleine Größe ist.
Hinweis: Trägheitsmoment einer Stange für Rotation um den Schwerpunkt ist
Lösungsweg:
a) Gesamte Drehmoment
Das Drehmoment
Am Stangenpendel greifen zwei Kräfte im Schwerpunkt an, die Gewichtskraft
Insgesamt wirkt auf das Stangenpendel also ein Drehmoment von
Wird die Kleinwinkelnäherung für
b) Bewegungsgleichung
Um die Bewegungsgleichung aufzustellen wird verwendet, dass
c) Frequenz
Die Schwingungsfrequenz
d) Ergebnis dimensionslos darstellen
Für den Fall, dass
Somit kann das Ergebnis dimensionslos dargestellt werden
wobei die Wurzel zu