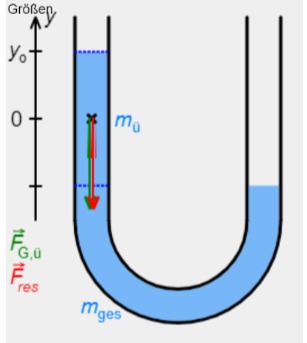
Ein Flüssigkeitspendel, auch bekannt als schwingende Flüssigkeitssäule, ist im Allgemeinen ein U-Rohr, in dem eine anfangs aus der Gleichgewichtslage ausgelenkte Flüssigkeitssäule schwingt. In der Abbildung sieht man den Aufbau des Versuchs.

1. Bestimmen Sie die Bewegungsgleichung.
   Beachten Sie, dass die Flüssigkeitssäule im U-Rohr einen Zylinder darstellt. Die Größen und lassen sich somit durch die Dichte der Flüssigkeit, die Querschnittsfläche A des U-Rohrs, und der Länge L ausdrücken.
2. Die Bewegungsgleichung ist eine Differentialgleichung Ordnung, die noch zwei Anfangsbedingungen zu ihrer kompletten Lösung erfordert. Gib diese beiden Anfangsbedingungen an.
3. Weisen Sie rechnerisch nach, dass die Zeit-Ort-Funktion mit geeignet gewähltem die Bewegungsgleichung erfüllt.
   Gib den geeigneten Term für an und bestimme den Wert so, dass diese ZeitOrt-Funktion auch die beiden Anfangsbedingungen erfüllt.
4. Die Flüssigkeitssäule eines Flüssigkeitspendels habe die Länge . Berechne die Schwinungsdauer dieses Flüssigkeitspendels.