48 / 64

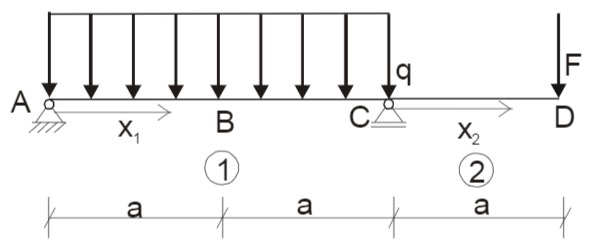
Aufgabenstellung:

Ein überkragender Balken (Länge const. wird durch eine Gleichstreckenlast q im Feld und durch eine Einzellast am Kragarmende belastet.

Gesucht: Für welches Verhältnis werden die Durchbiegungen in Feldmitte und am Kragarmende D gleich groß?

Gegeben:

Überkragender Balken mit Gleichstreckenlast q

 

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

1. Lösungsmöglichkeit mit Biegelinientafel

Skizze

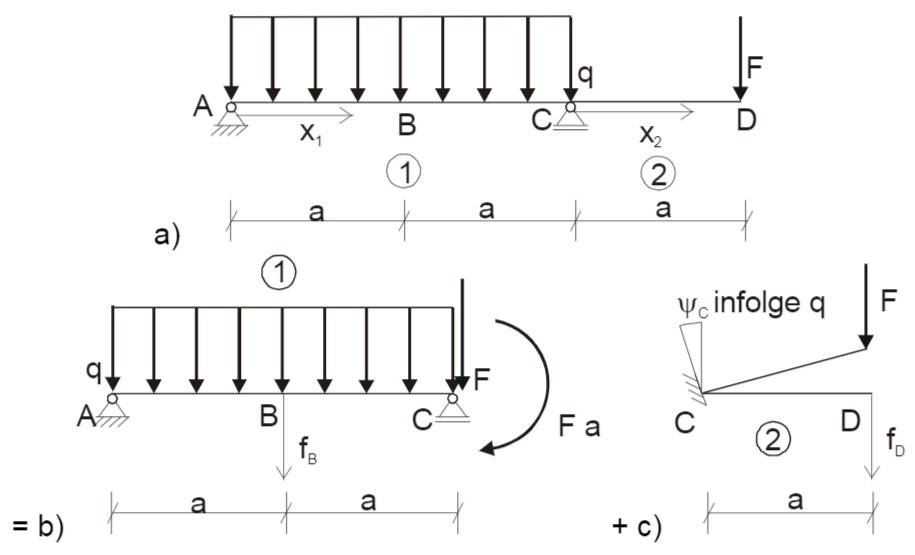
Abbildung

Die Absenkung setzt sich aus folgenden Anteilen zusammen

1. Absenkung in B infolge q

2. Absenkung in B infolge a

Die Absenkung setzt sich aus folgenden Anteilen zusammen

3. Absenkung in D infolge Verdrehung in C infolge q

4. Absenkung in D infolge Verdrehung in C infolge a

5. Absenkung in D infolge

Das Verhältis , für das die beiden Absenkungen gleich sind, ergibt sich aus
der Bedingung  

Die beiden Absenkungen sind gleich, wenn das Verhältnis ist

Lösungsmöglichkeit durch feldweise Integration

Es handelt sich um eine Zweibereichsaufgabe, deren Koordinaten für die beiden Bereiche die im Bild gegeben sind (Skizze):

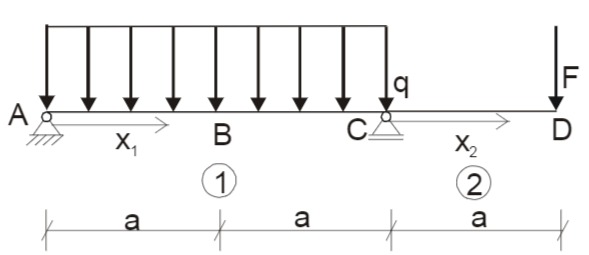
Abbildung

Die Integration der Differentialgleichungen führt auf die Verläufe in den Bereichen

Bereich 1 Bereich 2


Aus den statischen Randbedingungen folgt

Aus den geometrischen Randbedingungen folgt

Aus den statischen Übergangsbedingungen folgt

Aus den geometrischen Übergangsbedingungen folgt

Aufgelöst ergibt sich:

Eingesetzt ergeben sich die Biegelinien für die beiden Bereiche:

Für

Für

An der Stelle gilt:

Lösung: