KIT - Klausuren - TM2

TM 2 Sammlung

TUHH-TM2

Unterschied In/Homogen

Basis, Basiswechsel

Abbildungsmatrizen

Funktionen bestimmen

Geraden und Ebenen

Gruppen

lineare abbildung 

quadratische ergänzung

Baustatik 1

Anfangswertprobleme :)

Differentialgleichungen

basis 

QR-Algorithmus

QR-Zerlegung

Cholesky-Zerlegung

Bild & Urbild

Zweigstromanalyse

Transistor als Thermometer

Investment

Teilfolgen

Epsilon Delta Kriterium

prinzip der virtuellen verrückung 

Linear Kombination

Folgen, Reihen und Potenzreihen

Flächenpressung

Arbeit 

Cholesky Zerlegung

Polynomfunktionen beschreiben

Zu Maß-und Integrationstheorie: Majorisierte Konvergenz

Teilchenphysik und Festkörperphysik

Orthogonaltrajektorien

test

Taylorreihen

Regel von de L'Hopital

Mathe

KRAFT

Grenzwert Funktion 

Folgenkriterium

ϵ-δ Kriterium 

Beweis Stetigkeit 

Wahrheitstabelle

2x2 Matrix

Matrix invertieren

Basiswechselsatz

Lineare Abbildunge 

Vorderrad fahradgabel lagerkräfte berechnen 

Spannungsregelung

Jordan Normal Form

Test

Induktion 

Jordan-Normalform

Ansatz der Störfunktion zur Bestimmung der Partikulären Lösung

Kurvenintegral

dlg mithilfe inhomogenen linearen system lösen

Inverse einer Matrix

Gleichmäßige Stetigkeit

addition

Regel von L´Hospital

Lineare Abbildungen

dimension eines Untervektorraumes bestimmen

Stationäre Stoffübertragung

Polplan, Prinzip der virtuellen Verrückungen

komplexe Ungleichungen 

Bidualräume

Dualräume

Taylorpolynome

Kern und Basis

Diagonalisieren einer Matrix

Rekursive Folgen

Exponentialreihe

Darstellungsmatrizen

restglied

Basiswechsel

Gamma Funktion

Newton Verfahren

Randwertaufgabe

Numerische Integration: Trapez- und Simpsonregel

Funktionenfolgen

dualräume

Dualraum

Komplexe Nullstellen

Chemie

Natascha Kirchmann

Differentialquotient

Folgedefinition des Funktionslimes

Grenzwerte und Stetigkeit 

Komplexe Zahlen

Kern und Bild 

Direkte Summe 

Koordinaten 

Exponentielle Verzinsung

Lineare Verzinsung

Festverzinsliche Wertpapiere

<p>\[<br />\mathrm{w}_{2}(\mathrm{c})=\frac{1}{3} \frac{1}{\mathrm{El}_{2}} \mathrm{~F} \mathrm{c}^{2}(\mathrm{c}+\mathrm{b}) <br />\]</p>
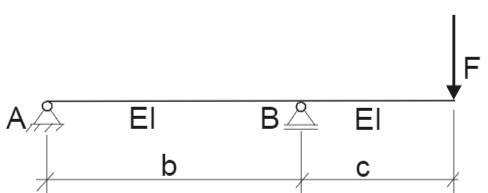
<p>\[<br />\psi_{1}(\mathrm{~b})=\psi_{2}(0)=\frac{1}{E \mathrm{I}_{2}} \frac{1}{3} \mathrm{~F} \ \mathrm{c}\ \mathrm{b} <br />\]</p>

<p>Es handelt sich um eine Zweibereichsaufgabe, deren Koordinaten für die beiden Bereiche im Bild gegeben sind. (Skizze):</p>


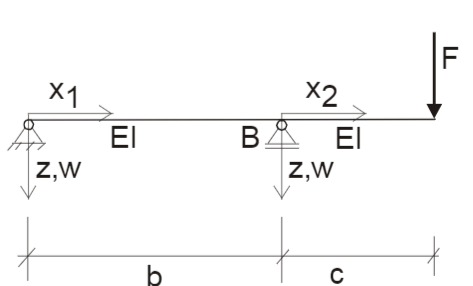
<p>Die Integration der Differentialgleichungen führt auf die Verläufe in den Bereichen</p>


<table style="border-collapse: collapse; width: 0%; height: auto;" border="1">
<tbody>
<tr>
<td style="width: 47.2174%;">
<p>Bereich 1</p>
</td>
<td style="width: 47.4031%;">
<p>Bereich 2</p>
</td>
</tr>
<tr>
<td style="width: 47.2174%;">
<p>\[<br />q\left(x_{1}\right)=0 <br />\]</p>
<p>\[<br />Q_{1}\left(x_{1}\right)=C_{11} <br />\]</p>
<p>\[<br />M_{1}\left(x_{1}\right)=C_{11} x_{1}+C_{21} <br />\]</p>
<p>\[<br />\psi_{1}\left(\mathrm{x}_{1}\right)=\frac{1}{\mathrm{E} I_{1}}\left(\frac{1}{2} \mathrm{C}_{11} \mathrm{x}_{1}^{2}+\mathrm{C}_{21} \mathrm{X}_{1}+\mathrm{C}_{31}\right) <br />\]</p>
<p>\[<br />w_{1}\left(x_{1}\right)=-\frac{1}{E I_{1}}\left(\frac{1}{6} C_{11} x_{1}^{3}+\frac{1}{2} C_{21} x_{1}^{2}\right. <br /> \left.+C_{31} x_{1}+C_{41}\right) \]</p>
</td>
<td style="width: 47.4031%;">
<p>\[<br />q\left(x_{2}\right)=0 <br />\]</p>
<p>\[<br />Q_{2}\left(x_{2}\right)=C_{12} <br />\]</p>
<p>\[</p>
<p><br />M_{2}\left(x_{2}\right)=C_{12} x_{2}+C_{22} <br />\]</p>
<p>\[<br />\psi_{2}\left(\mathrm{x}_{2}\right)=\frac{1}{\mathrm{E} I_{2}}\left(\frac{1}{2} \mathrm{C}_{12} \mathrm{x}_{2}^{2}+\mathrm{C}_{22} \mathrm{x}_{2}+\mathrm{C}_{32}\right) <br />\]</p>
<p>\[<br />\mathrm{w}_{2}\left(\mathrm{x}_{2}\right)=-\frac{1}{\mathrm{E} I_{2}}\left(\frac{1}{6} \mathrm{C}_{12} \mathrm{x}_{2}^{3}+\frac{1}{2} \mathrm{C}_{22} \mathrm{x}_{2}^{2}+\mathrm{C}_{32}\right. <br />\left.\mathrm{x}_{2}+\mathrm{C}_{42}\right) <br />\]</p>
</td>
</tr>
</tbody>
</table>


<p>Die Konstanten werden über die Randbedingungen bestimmt.</p>


<p>\[<br />M_{1}\left(x_{1}=0\right)=0\quad \Rightarrow C_{21}=0 <br />\]</p>


<p>\[<br />\mathrm{Q}_{2}\left(\mathrm{x}_{2}=\mathrm{c}\right)=\mathrm{F} \quad \Rightarrow \mathrm{C}_{12}=\mathrm{F}\]</p>


<p>\[M_{2}\left(x_{2}=c\right)=0 \quad \Rightarrow C_{22}=-C_{12} c=-F c\]</p>


<p>\[<br />w_{1}\left(x_{1}=0\right)=0 \quad \Rightarrow C_{41}=0 <br />\]</p>


<p>\[w_{1}\left(x_{1}=b\right)=0 \quad \Rightarrow \frac{1}{6} C_{11} b^{2}+C_{31}=0\]</p>


<p>\[\mathrm{w}_{2}\left(\mathrm{x}_{2}=0\right)=0 \quad\Rightarrow \mathrm{C}_{42}=0 <br />\]</p>


<p>Nutze für die restlichen Konstanten Übergangsbedingungen:</p>


<p>Aus den geometrische Übergangsbedingungen folgt</p>


<p>\[<br />\psi_{1}\left(\mathrm{x}_{1}=\mathrm{b}\right)=\psi_{2}\left(\mathrm{x}_{2}=0\right) \]</p>
<p>\[\Rightarrow \frac{1}{\mathrm{EI}_{1}}\left(\frac{1}{2} \mathrm{C}_{11} \mathrm{~b}^{2}+\mathrm{C}_{31}\right)=\frac{1}{\mathrm{EI}_{2}} \mathrm{C}_{32} <br />\]</p>


<p>Mit \( \mathrm{El}_{1}=\mathrm{E} \mathrm{I}_{2} \) folgt weiter</p>


<p>Mit <mjx-container class="MathJax" jax="SVG"><svg alt=" \mathrm{El}_{1}=\mathrm{E} \mathrm{I}_{2} " style="vertical-align: -0.339ex" xmlns="http://www.w3.org/2000/svg" width="9.52ex" height="1.91ex" role="img" focusable="false" viewBox="0 -694 4207.7 844" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-1011-TEX-N-45" d="M128 619Q121 626 117 628T101 631T58 634H25V680H597V676Q599 670 611 560T625 444V440H585V444Q584 447 582 465Q578 500 570 526T553 571T528 601T498 619T457 629T411 633T353 634Q266 634 251 633T233 622Q233 622 233 621Q232 619 232 497V376H286Q359 378 377 385Q413 401 416 469Q416 471 416 473V493H456V213H416V233Q415 268 408 288T383 317T349 328T297 330Q290 330 286 330H232V196V114Q232 57 237 52Q243 47 289 47H340H391Q428 47 452 50T505 62T552 92T584 146Q594 172 599 200T607 247T612 270V273H652V270Q651 267 632 137T610 3V0H25V46H58Q100 47 109 49T128 61V619Z"></path><path id="MJX-1011-TEX-N-6C" d="M42 46H56Q95 46 103 60V68Q103 77 103 91T103 124T104 167T104 217T104 272T104 329Q104 366 104 407T104 482T104 542T103 586T103 603Q100 622 89 628T44 637H26V660Q26 683 28 683L38 684Q48 685 67 686T104 688Q121 689 141 690T171 693T182 694H185V379Q185 62 186 60Q190 52 198 49Q219 46 247 46H263V0H255L232 1Q209 2 183 2T145 3T107 3T57 1L34 0H26V46H42Z"></path><path id="MJX-1011-TEX-N-31" d="M213 578L200 573Q186 568 160 563T102 556H83V602H102Q149 604 189 617T245 641T273 663Q275 666 285 666Q294 666 302 660V361L303 61Q310 54 315 52T339 48T401 46H427V0H416Q395 3 257 3Q121 3 100 0H88V46H114Q136 46 152 46T177 47T193 50T201 52T207 57T213 61V578Z"></path><path id="MJX-1011-TEX-N-3D" d="M56 347Q56 360 70 367H707Q722 359 722 347Q722 336 708 328L390 327H72Q56 332 56 347ZM56 153Q56 168 72 173H708Q722 163 722 153Q722 140 707 133H70Q56 140 56 153Z"></path><path id="MJX-1011-TEX-N-49" d="M328 0Q307 3 180 3T32 0H21V46H43Q92 46 106 49T126 60Q128 63 128 342Q128 620 126 623Q122 628 118 630T96 635T43 637H21V683H32Q53 680 180 680T328 683H339V637H317Q268 637 254 634T234 623Q232 620 232 342Q232 63 234 60Q238 55 242 53T264 48T317 46H339V0H328Z"></path><path id="MJX-1011-TEX-N-32" d="M109 429Q82 429 66 447T50 491Q50 562 103 614T235 666Q326 666 387 610T449 465Q449 422 429 383T381 315T301 241Q265 210 201 149L142 93L218 92Q375 92 385 97Q392 99 409 186V189H449V186Q448 183 436 95T421 3V0H50V19V31Q50 38 56 46T86 81Q115 113 136 137Q145 147 170 174T204 211T233 244T261 278T284 308T305 340T320 369T333 401T340 431T343 464Q343 527 309 573T212 619Q179 619 154 602T119 569T109 550Q109 549 114 549Q132 549 151 535T170 489Q170 464 154 447T109 429Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="msub"><g data-mml-node="TeXAtom" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="45" xlink:href="#MJX-1011-TEX-N-45"></use><use data-c="6C" xlink:href="#MJX-1011-TEX-N-6C" transform="translate(681,0)"></use></g></g><g data-mml-node="TeXAtom" transform="translate(992,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mn"><use data-c="31" xlink:href="#MJX-1011-TEX-N-31"></use></g></g></g><g data-mml-node="mo" transform="translate(1673.3,0)"><use data-c="3D" xlink:href="#MJX-1011-TEX-N-3D"></use></g><g data-mml-node="TeXAtom" data-mjx-texclass="ORD" transform="translate(2729.1,0)"><g data-mml-node="mi"><use data-c="45" xlink:href="#MJX-1011-TEX-N-45"></use></g></g><g data-mml-node="msub" transform="translate(3410.1,0)"><g data-mml-node="TeXAtom" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="49" xlink:href="#MJX-1011-TEX-N-49"></use></g></g><g data-mml-node="TeXAtom" transform="translate(394,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mn"><use data-c="32" xlink:href="#MJX-1011-TEX-N-32"></use></g></g></g></g></g></svg></mjx-container> folgt weiter</p>


<p>Mit den statische Übergangsbedingungen folgt</p>


<p>\[<br />M_{1}\left(x_{1}=b\right)=M_{2}\left(x_{2}=0\right) \]</p>


<p>\[\Rightarrow C_{11} b+0=C_{22}=-c F <br />\]</p>


<p>Die Biegelinie im Bereich 2 lautet</p>


<p>\[<br />w_{2}\left(x_{2}\right)=-\frac{1}{E \mathrm{I}_{2}}\left(\frac{1}{6} F x_{2}^{3}-\frac{1}{2} F c x_{2}^{2}+\frac{1}{3} c b F x_{2}\right) <br />\]</p>


<p>Damit ist die Durchbiegung des Lastangriffspunktes</p>


<p>\[<br />\mathrm{w}_{2}(\mathrm{c})=-\frac{1}{E \mathrm{I}_{2}} \mathrm{~F} \mathrm{c}^{2}\left(\frac{1}{6} \mathrm{c}-\frac{1}{2} \mathrm{c}-\frac{1}{3} \mathrm{~b}\right)=\frac{1}{3} \frac{1}{\mathrm{El}_{2}} \mathrm{~F} \mathrm{c}^{2}(\mathrm{c}+\mathrm{b}) <br />\]</p>


<p>und der Winkel am Lager \( \mathrm{B} \)</p>


<p>und der Winkel am Lager <mjx-container class="MathJax" jax="SVG"><svg alt=" \mathrm{B} " style="vertical-align: 0" xmlns="http://www.w3.org/2000/svg" width="1.602ex" height="1.545ex" role="img" focusable="false" viewBox="0 -683 708 683" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-1021-TEX-N-42" d="M131 622Q124 629 120 631T104 634T61 637H28V683H229H267H346Q423 683 459 678T531 651Q574 627 599 590T624 512Q624 461 583 419T476 360L466 357Q539 348 595 302T651 187Q651 119 600 67T469 3Q456 1 242 0H28V46H61Q103 47 112 49T131 61V622ZM511 513Q511 560 485 594T416 636Q415 636 403 636T371 636T333 637Q266 637 251 636T232 628Q229 624 229 499V374H312L396 375L406 377Q410 378 417 380T442 393T474 417T499 456T511 513ZM537 188Q537 239 509 282T430 336L329 337H229V200V116Q229 57 234 52Q240 47 334 47H383Q425 47 443 53Q486 67 511 104T537 188Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="TeXAtom" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="42" xlink:href="#MJX-1021-TEX-N-42"></use></g></g></g></g></svg></mjx-container></p>


<p>\[<br />\psi_{1}(\mathrm{~b})=\psi_{2}(0)=\frac{1}{E \mathrm{I}_{2}} \frac{1}{3} \mathrm{~F} \ \mathrm{c}\ \mathrm{b} <br />\]</p>

<div class="horizontalLayoutContainer" style="display: flex; flex-direction: row;">
<div class="horizontalLayoutElement" style="padding-right: 10px; flex: 1;">
<p>Ein überkragender Balken (E I = const.) ist am freien Ende durch eine Einzelkraft F belastet.</p>
<p> </p>
<p><strong>Gesucht: </strong>Bestimmung der Durchbiegung am freien Ende infolge \( \mathrm{F} \) und der Neigung (Betrag des Winkels) am Lager B.</p>
<p><strong>Gegeben:</strong> \( b,\ c,\ F \)</p>
</div>
<div class="horizontalLayoutElement" style="padding-left: 10px; flex: 1;">
<p class="horizontalLayoutText"><img src="https://storage.googleapis.com/max-academy-image-bucket/609f9484fd648ba8097cf59c.png" alt="Überkragender Balken mit Einzelkraft F" width="318" height="126" /></p>
</div>
</div>
<p> </p>

<div class="horizontalLayoutContainer" style="display: flex; flex-direction: row;">
<div class="horizontalLayoutElement" style="padding-right: 10px; flex: 1;">
<p>Ein überkragender Balken (E I = const.) ist am freien Ende durch eine Einzelkraft F belastet.</p>
<p> </p>
<p><strong>Gesucht: </strong>Bestimmung der Durchbiegung am freien Ende infolge <mjx-container class="MathJax" jax="SVG"><svg alt=" \mathrm{F} " style="vertical-align: 0" xmlns="http://www.w3.org/2000/svg" width="1.477ex" height="1.538ex" role="img" focusable="false" viewBox="0 -680 653 680" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-991-TEX-N-46" d="M128 619Q121 626 117 628T101 631T58 634H25V680H582V676Q584 670 596 560T610 444V440H570V444Q563 493 561 501Q555 538 543 563T516 601T477 622T431 631T374 633H334H286Q252 633 244 631T233 621Q232 619 232 490V363H284Q287 363 303 363T327 364T349 367T372 373T389 385Q407 403 410 459V480H450V200H410V221Q407 276 389 296Q381 303 371 307T348 313T327 316T303 317T284 317H232V189L233 61Q240 54 245 52T270 48T333 46H360V0H348Q324 3 182 3Q51 3 36 0H25V46H58Q100 47 109 49T128 61V619Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="TeXAtom" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="46" xlink:href="#MJX-991-TEX-N-46"></use></g></g></g></g></svg></mjx-container> und der Neigung (Betrag des Winkels) am Lager B.</p>
<p><strong>Gegeben:</strong> <mjx-container class="MathJax" jax="SVG"><svg alt=" b,\ c,\ F " style="vertical-align: -0.439ex" xmlns="http://www.w3.org/2000/svg" width="6.788ex" height="2.009ex" role="img" focusable="false" viewBox="0 -694 3000.3 888" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-992-TEX-I-1D44F" d="M73 647Q73 657 77 670T89 683Q90 683 161 688T234 694Q246 694 246 685T212 542Q204 508 195 472T180 418L176 399Q176 396 182 402Q231 442 283 442Q345 442 383 396T422 280Q422 169 343 79T173 -11Q123 -11 82 27T40 150V159Q40 180 48 217T97 414Q147 611 147 623T109 637Q104 637 101 637H96Q86 637 83 637T76 640T73 647ZM336 325V331Q336 405 275 405Q258 405 240 397T207 376T181 352T163 330L157 322L136 236Q114 150 114 114Q114 66 138 42Q154 26 178 26Q211 26 245 58Q270 81 285 114T318 219Q336 291 336 325Z"></path><path id="MJX-992-TEX-N-2C" d="M78 35T78 60T94 103T137 121Q165 121 187 96T210 8Q210 -27 201 -60T180 -117T154 -158T130 -185T117 -194Q113 -194 104 -185T95 -172Q95 -168 106 -156T131 -126T157 -76T173 -3V9L172 8Q170 7 167 6T161 3T152 1T140 0Q113 0 96 17Z"></path><path id="MJX-992-TEX-N-A0" d=""></path><path id="MJX-992-TEX-I-1D450" d="M34 159Q34 268 120 355T306 442Q362 442 394 418T427 355Q427 326 408 306T360 285Q341 285 330 295T319 325T330 359T352 380T366 386H367Q367 388 361 392T340 400T306 404Q276 404 249 390Q228 381 206 359Q162 315 142 235T121 119Q121 73 147 50Q169 26 205 26H209Q321 26 394 111Q403 121 406 121Q410 121 419 112T429 98T420 83T391 55T346 25T282 0T202 -11Q127 -11 81 37T34 159Z"></path><path id="MJX-992-TEX-I-1D439" d="M48 1Q31 1 31 11Q31 13 34 25Q38 41 42 43T65 46Q92 46 125 49Q139 52 144 61Q146 66 215 342T285 622Q285 629 281 629Q273 632 228 634H197Q191 640 191 642T193 659Q197 676 203 680H742Q749 676 749 669Q749 664 736 557T722 447Q720 440 702 440H690Q683 445 683 453Q683 454 686 477T689 530Q689 560 682 579T663 610T626 626T575 633T503 634H480Q398 633 393 631Q388 629 386 623Q385 622 352 492L320 363H375Q378 363 398 363T426 364T448 367T472 374T489 386Q502 398 511 419T524 457T529 475Q532 480 548 480H560Q567 475 567 470Q567 467 536 339T502 207Q500 200 482 200H470Q463 206 463 212Q463 215 468 234T473 274Q473 303 453 310T364 317H309L277 190Q245 66 245 60Q245 46 334 46H359Q365 40 365 39T363 19Q359 6 353 0H336Q295 2 185 2Q120 2 86 2T48 1Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mi"><use data-c="1D44F" xlink:href="#MJX-992-TEX-I-1D44F"></use></g><g data-mml-node="mo" transform="translate(429,0)"><use data-c="2C" xlink:href="#MJX-992-TEX-N-2C"></use></g><g data-mml-node="mtext" transform="translate(873.7,0)"><use data-c="A0" xlink:href="#MJX-992-TEX-N-A0"></use></g><g data-mml-node="mi" transform="translate(1123.7,0)"><use data-c="1D450" xlink:href="#MJX-992-TEX-I-1D450"></use></g><g data-mml-node="mo" transform="translate(1556.7,0)"><use data-c="2C" xlink:href="#MJX-992-TEX-N-2C"></use></g><g data-mml-node="mtext" transform="translate(2001.3,0)"><use data-c="A0" xlink:href="#MJX-992-TEX-N-A0"></use></g><g data-mml-node="mi" transform="translate(2251.3,0)"><use data-c="1D439" xlink:href="#MJX-992-TEX-I-1D439"></use></g></g></g></svg></mjx-container></p>
</div>
<div class="horizontalLayoutElement" style="padding-left: 10px; flex: 1;">
<p class="horizontalLayoutText"><img src="https://storage.googleapis.com/max-academy-image-bucket/609f9484fd648ba8097cf59c.png" alt="Überkragender Balken mit Einzelkraft F" width="318" height="126" /></p>
</div>
</div>
<p> </p>

Dies ist eine interaktive Aufgabe zu: TM 2 Sammlung mit praktischen Tipps zum Lösen und einer Zusammenfassung der nötigen Theorie

Aufgabenstellung:

Lösungsweg:

Lösung: