Aufgabenstellung:
Auf eine einseitig fest eingespannte Hohlwelle ist ein Ring aufgeschrumpft. Dieser Ring wird in Umfangsrichtung so stark belastet, dass er auf der Welle rutscht. Dabei wird auf die Welle das Moment
Gegeben:
Gesucht: Bestimmung der Querschnittsverdrehungen

Lösungsweg:
Es handelt sich um eine statisch bestimmte Zweibereichsaufgabe, deren Koordinaten im folgendem Bild zu entnehmen sind (Skizze anfertigen):
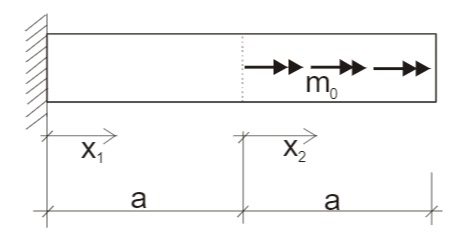
Nach Integration für Bereich 1 und Bereich 2 folgen die Gleichungen für den Torsionsmomenten- und Verdrehungsverlauf.
Für Bereich 1 gilt
für Bereich 2 gilt
Mit den Rand- und Übergangsbedingungen lassen sich die Konstanten bestimmen
Der Torsionsmomenten- und Verdrehungsverlauf ist für beide Bereiche bestimmt
Skizze des Verdrehungsverlaufes
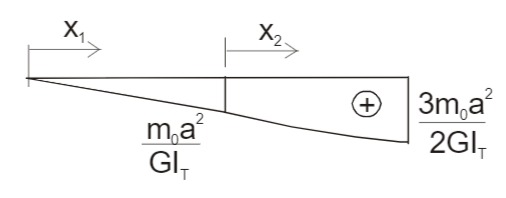
Der Maximalwert für die Verdrehung ergibt sich an der Stelle
Die Maximalspannung ist gleich der maximalen Schubspannung. Diese entsteht am Rand des Querschnitts
Im ersten Bereich ist die Schubspannung konstant und größer als im Bereich 2
Lösung:
Der Maximalwert für die Verdrehung ergibt sich an der Stelle