Aufgabenstellung:
Eine beidseitig eingespannte Welle besteht aus zwei Vollquerschnitten unterschiedlichen Materials und Durchmessers. Sie ist in der Mitte durch ein Torsionsmoment belastet.
Gegeben:
Gesucht: Bestimmung der Einspannmomente, der Schubspannungsverläufe und der Verdrehung in Wellenmitte (Punkt C)

Lösungsweg:
Skizze
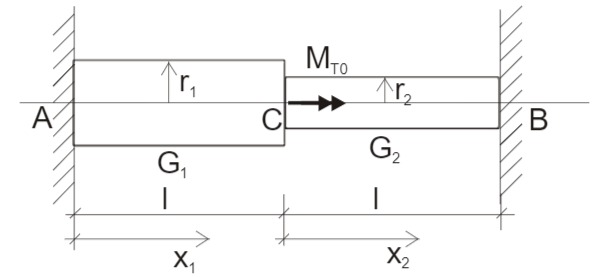
Für Bereich 1 gilt
für Bereich 2 gilt
Skizze Übergangsstelle
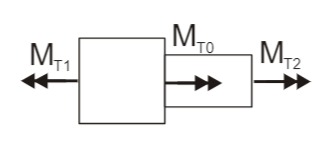
Für die beiden Konstanten
Sonst sind keine statischen Randbedingungen vorhanden. Es stehen aber zwei geometrische Randbedingungen und eine geometrische Übergangsbedingung zur Verfügung.
daraus folgt
Daraus folgt
Daraus ergeben sich nun die Schubspannungsverläufe mit
Die maximale Schubspannung ergeben sich somit als
mit
Die Verdrehungen der Querschnitte sind
Damit ergibt sich die Verdrehung in Stabmitte im Punkt C zu
Skizze Torsionsmoment
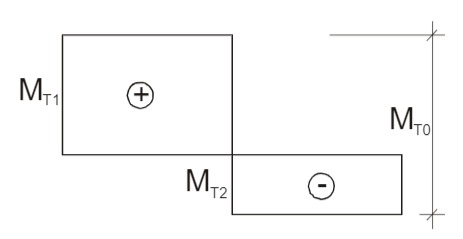
2. Lösungsmöglichkeit mit dem Arbeitssatz
Es handelt sich um eine sehr übersichtliche Lösungsmethode, die auch für die Verformung unter Torsion herangezogen werden kann. Mit zwei unterschiedlichen Lösungswegen wird der Arbeitssatz dargestellt.
Aufschneiden am rechten Lager (Skizze):
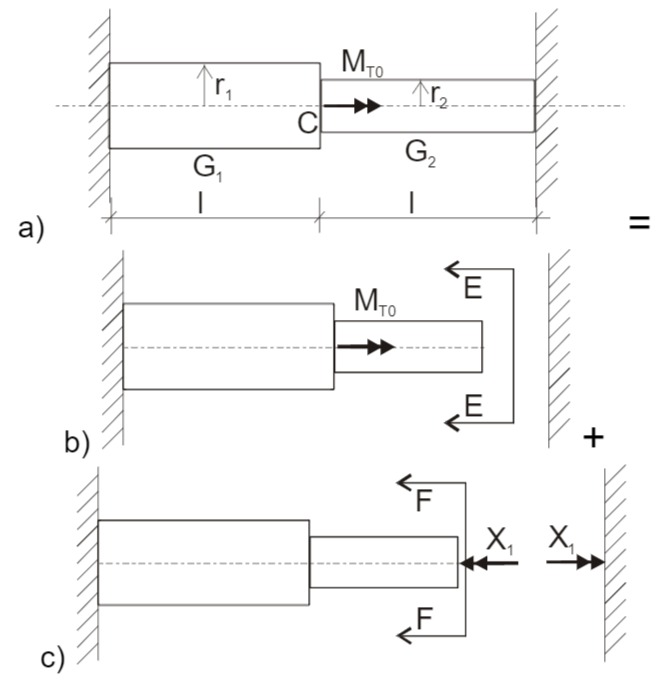
Skizze der Querschnitte und Verdrehung:
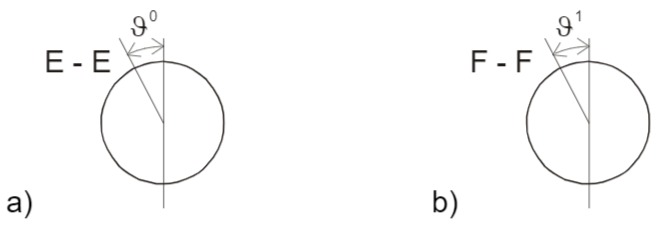
Die Querschnittsverdrehungen ergeben sich zu
Die Kompatibilitätsbedingung lautet
Die Verdrehungen der beiden Wellen muß an der Übergangsstelle gleich groß sein. Es darf nichts überlappen oder klaffen. Daraus folgt
Für
Arbeitssatz mit Aufschneiden in Wellenmitte
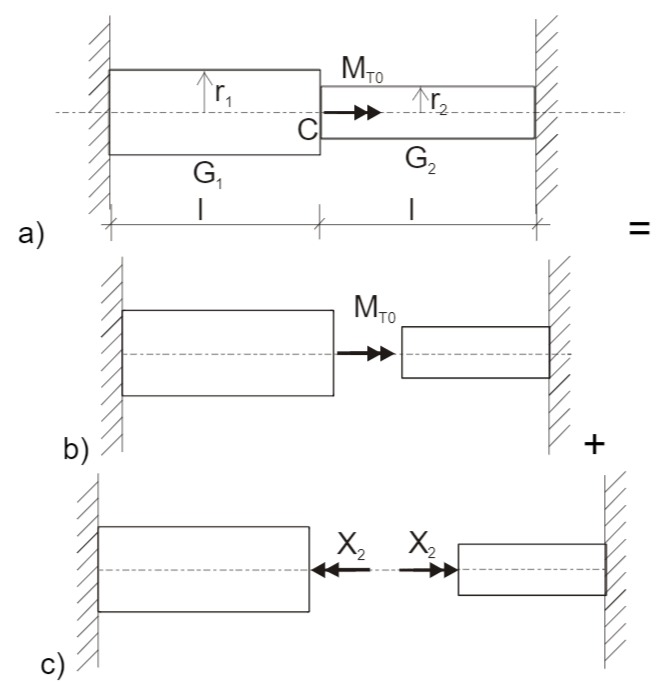
Die Schnittmomente in Wellenmitte lauten
Die Querschnittsverdrehungen in Wellenmitte sind
Die Kompatibilitätsbedingung lautet
Die Verdrehungen der beiden Wellen muß an der Übergangsstelle gleich groß sein. Es darf nichts überlappen oder klaffen. Das ergibt
Es ergibt sich für
Daraus ergeben sich die Torsionsmomente, die Verdrehung am Stabende und die Schubspannungen
Lösung: