Aufgabenstellung:
Gegeben ist die in der Abbildung dargestellte Leiterplatte (grau hinterlegter Bereich) mit parallel zur
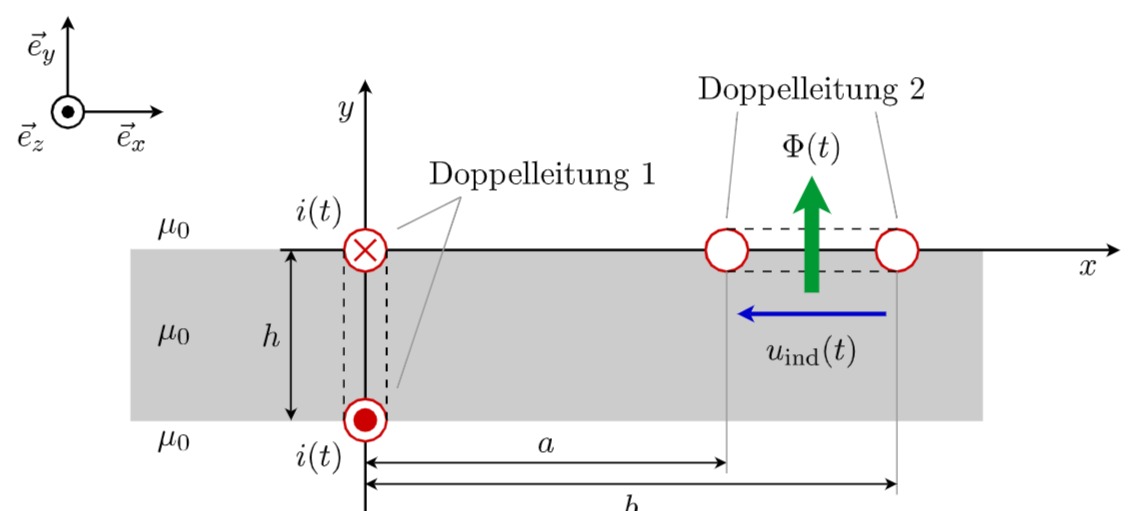
Der Hinleiter von Doppelleitung 1 befinde sich auf der Oberseite der Leiterplatte, während der Rückleiter auf der Unterseite verläuft. Die Doppelleitung 1 wird in der gezeigten Richtung vom Strom
- Bestimmen Sie den magnetischen Fluss
durch die Doppelleitung 2 infolge des durch die Doppelleitung fließenden Stroms . - Geben Sie die Gegeninduktivität
zwischen Doppelleitung 1 und Doppelleitung 2 an.
Die Doppelleitung 1 werde nun vom Stromdurchflossen. - Berechnen Sie die zwischen den offenen Klemmen von Doppelleitungen 2 induzierte Spannung
Lösungsweg:
Aufgabenteil a) magnetischen Fluss
Der Gesamtfluss setzt sich zusammen aus der Überlagerung der beiden Teilflüsse infolge der beiden Leiter von Doppelleitung 1. Fluss
Abbildung: Geometrische Anordnung
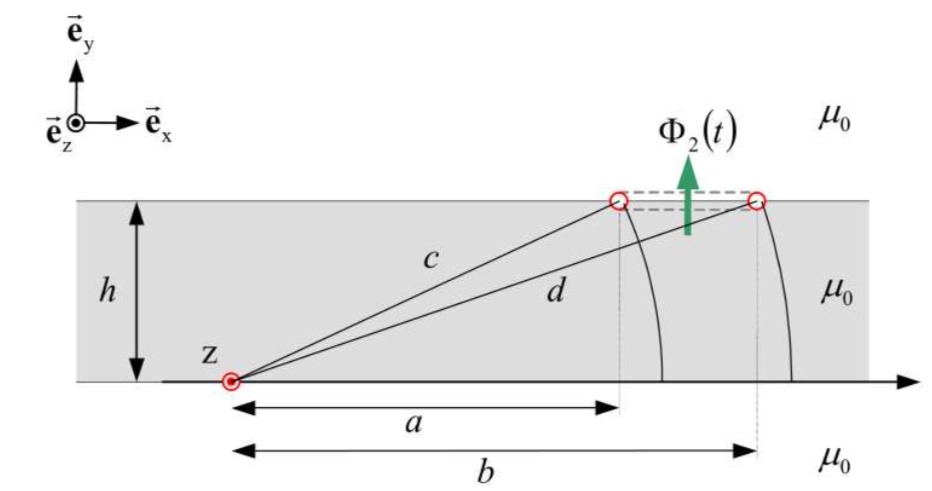
Für den 2. Leiter der Doppelleitung 1 ergibt sich ein identisches Vorgehen. Wird das koordinatensystem so verschoben, dass der 2 . Leiter jetzt im Ursprung liegt, dann gilt mit den in der folgenden Abbildung definierten Abständen
Für den Gesamtfluss gilt:
Aufgabenteil b) Gegeninduktivität:
Aufgabenteil
Bemerkung: Das Vorzeichen ist wegen der zweidimensionalen Darstellung nicht eindeutig.