Aufgabenstellung:
Gegeben ist der verzweigte magnetische Kreis. Der Eisenkern ist in drei Abschnitte mit den mittleren Längen
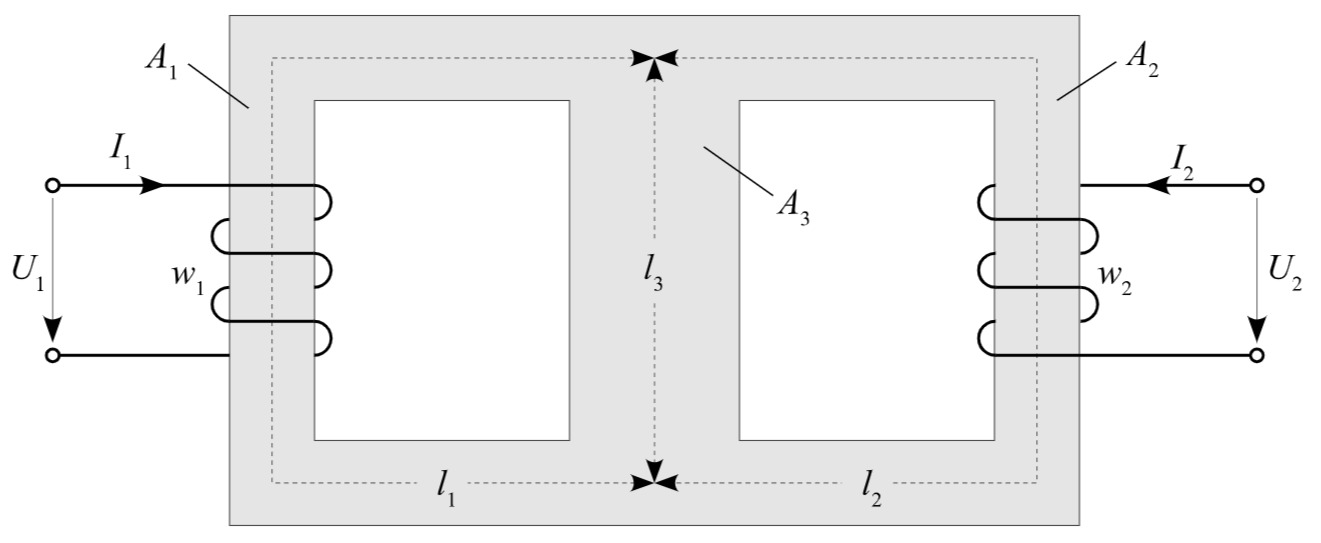
Bestimmen Sie:
a) das zu dem magnetischen Kreis äquivalente Ersatzschaltbild mit seinen magnetischen Widerständen
b) die magnetischen Flüsse in den drei Abschnitten des Eisenkerns.
c) die Eigeninduktivitäten
d) die Gegeninduktivität
Lösungsweg:
a) Ersatzschaltbild & Widerstand
Im ersten Schritt weisen wir den magnetischen Flüssen in den drei Abschnitten eine Zählrichtung zu. Die Richtung des magnetischen Flusses erhält man mit Hilfe der,"Rechten Hand Regel", in Abhängigkeit von der Stromrichtung und dem Wickelsinn der Spule. Umfasst man die Spule derart mit der rechten Hand, dass die Finger in die Zählrichtung des Stromes zeigen, so zeigt der Daumen in die Richtung des magnetischen Feldes.
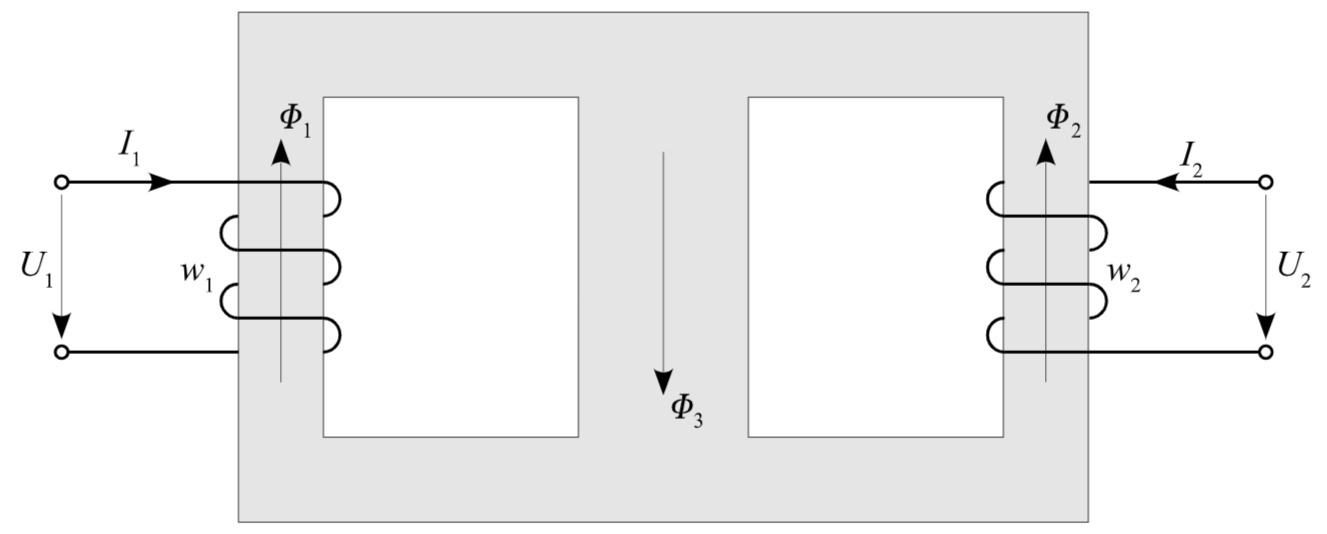
Wendet man diese Regel auf den gegebenen magnetischen Kreis an, so ergibt es sich, dass bei beiden Spulen die magnetische Feldstärke nach oben zeigt. Zweckmäßigerweise wählt man für den magnetischen Fluss
Unter der Voraussetzung, die bei magnetischen Kreisen mit einem Kern hoher Permeabilität praktisch gegeben ist, dass das Magnetfeld außerhalb des Eisens Null ist, lässt sich für einen solchen Kreis ein Ersatzschaltbild angeben, welches genauso wie ein Netzwerk mit Ohmschen Widerständen behandelt werden kann. Die elektrischen Größen werden lediglich durch magnetische Größen ersetzt.
Hinweis:
Hinweis:
Oft findet man für die magnetische Spannung
Damit gelangt man zu dem folgenden Ersatzschaltbild.
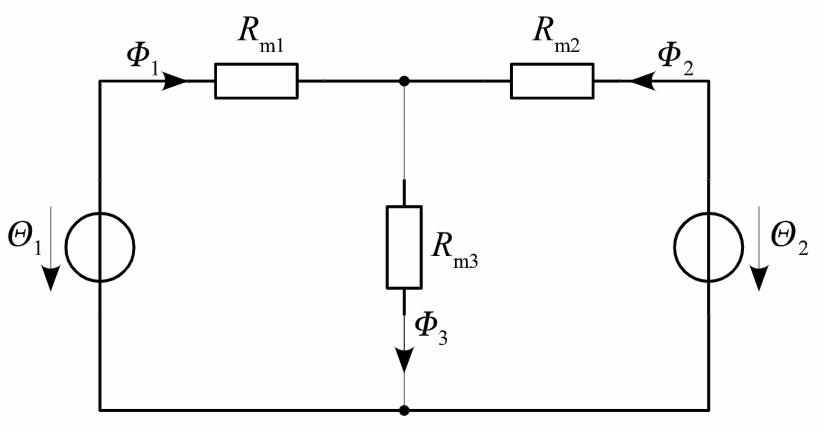
Der magnetische Widerstand eines Eisenschenkels berechnet sich in gleicher Weise wie der elektrische Widerstand eines stabförmigen Leiters. Der Widerstand ist um so größer, je größer die Länge des Stabs ist und um so kleiner je größer der Querschnitt ist. Eine große relative Permeabilität des Materials erniedrigt den magnetischen Widerstand ebenso wie eine hohe spezifische Leitfähigkeit den elektrischen Widerstand erniedrigt. Daraus ergibt sich für die magnetischen Widerstände
Die magnetischen Spannungsquellen sind gleich den magnetischen Durchflutungen
b) Magnetisches Flüsse
Die magnetischen Flüsse können nun wie Ströme in einem normalen elektrischen Netzwerk berechnet werden. Dazu werden zwei Maschengleichungen und eine Knotengleichung aufgestellt.
Die drei Gleichungen (1) bis (3) lassen sich auch als Matrizengleichung darstellen. Die Darstellung in Matrizenform bringt zwar keinen Vorteil für den Lösungsweg, erhöht aber die Übersichtlichkeit.
Zur Bestimmung der magnetischen Flüsse, berechnen wir zuerst die Determinante des Gleichungssystems.
Die magnetischen Flüsse ergeben sich dann mit der Determinantenregel zu
c) Eigeninduktivität
Die Eigeninduktivität einer Spule ist definiert als das Verhältnis von dem magnetischen Fluss. der die von den Windungen der Spule aufgespannte Fläche durchsetzt, zu dem Strom, der die Spule durchfließt und den Fluss erzeugt. Da der von dem Eisenkern geführte Fluss jede einzelne Windung durchsetzt, muss dieser Fluss
Den magnetischen Fluss
Ersetzt man
Die Induktivität
Ersetzt man
d) Gegeninduktivität
Die Gegeninduktivität zweier Spulen ist definiert als das Verhältnis von dem magnetischen Fluss, der die von den Windungen der Spule l aufgespannte Fläche durchsetzt, zu dem Strom, der die Spule 2 durchfließt und den Fluss erzeugt. Es ist sehr wichtig zu beachten, dass nur der Anteil des magnetischen Flusses berücksichtigt wird, der von der stromdurchflossenen Spule 2 verursacht wird. Vertauscht man die Rollen von Spule 1 und 2 , so ergibt sich für die Gegeninduktivität der gleiche Wert wie im ersten Fall.
Für
Lösung:
a)
Ersatzschaltbild siehe Lösungsweg
b)
c)
d)