Aufgabenstellung:
Gegeben ist eine Anordnung aus zwei konzentrisch gewickelen Luftspulen mit kreisförmigem Querschnitt und gleicher Länge
- Beide Spulen werden in gleicher Richtung von einem Gleichstrom
durchflossen. Berechnen Sie die magnetische Feldstärke und die magnetische Induktion innerhalb und außerhalb der Spulen mit den für lange Zylinderspulen üblichen Näherungen. - Bestimmen Sie die Selbstinduktion und die Gegeninduktion der Anordnung! Leiten Sie zunächst allgemein die Beziehungen zur Ermittlung von Selbst- und Gegeninduktivität her.
Abbildung: Querschnitt durch die Spulenanordnung
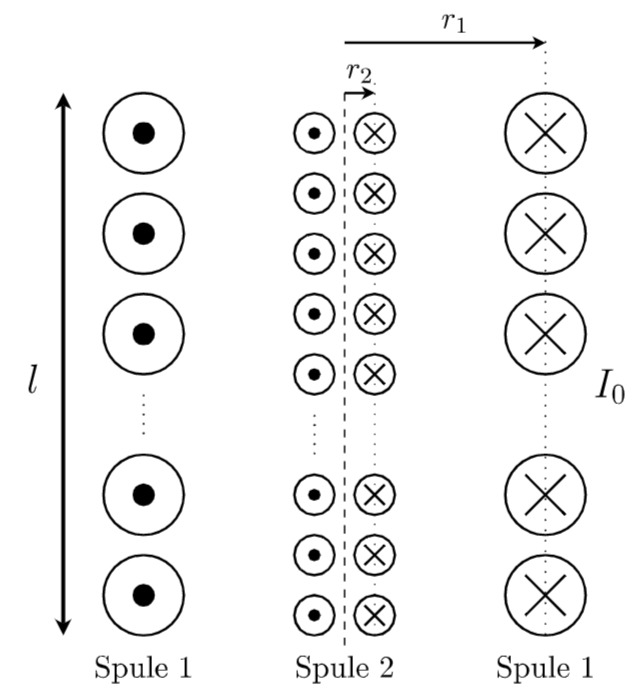
Lösungsweg:
Aufgabenteil a:
Vorgehensweise:
- Festlegen der zu nutzenden Näherungen
- Bestimmen der magnetischen Feldstärke der Spulen
- Betrachten der einzelnen Raumgebiete
- Herleitung der Formel für die Selbstinduktivität
Näherungen
Aus dieser Näherung folgt, dass das Induktionsfeld im inneren der Spule näherungsweise homogen ist. - Vernachlässigung von Streufeldern: Streufelder treten nur an den Rändern auf. Sie können aufgrund der ersten Näherung als klein gegenüber dem Feld im Inneren der Spule angesehen und somit vernachlässigt werden.
Die magnetischen Feldlinien teilen sich im Außenraum der Spule bis ins Unendliche auf. Die Feldstärke im einzelnen kleinen Raumelement ist daher Null. - Konstantes Feld im Innenraum der Spule
- Leiterdurchmesser
Allgemeine Berechnung der magnetischen Feldstärke einer Spule
Das allgemeine Durchflutungsgesetz lautet:
Wir können hier den Weg wie in der Abbildung gezeigt, in 4 Teilwege zerlegen. Diese Wege können dann einzeln integriert werden. Der Weg bildet hier mit dem Strom durch die Spule ein Rechtssystem. Wir erhalten somit die folgenden Integrale:
Da im Außenraum die magnetische Feldstärke laut der Näherungen verschwindet, gilt
Abbildung Integrationsweg: Stromrichtung und Umlaufweg ergeben ein Rechtssystem
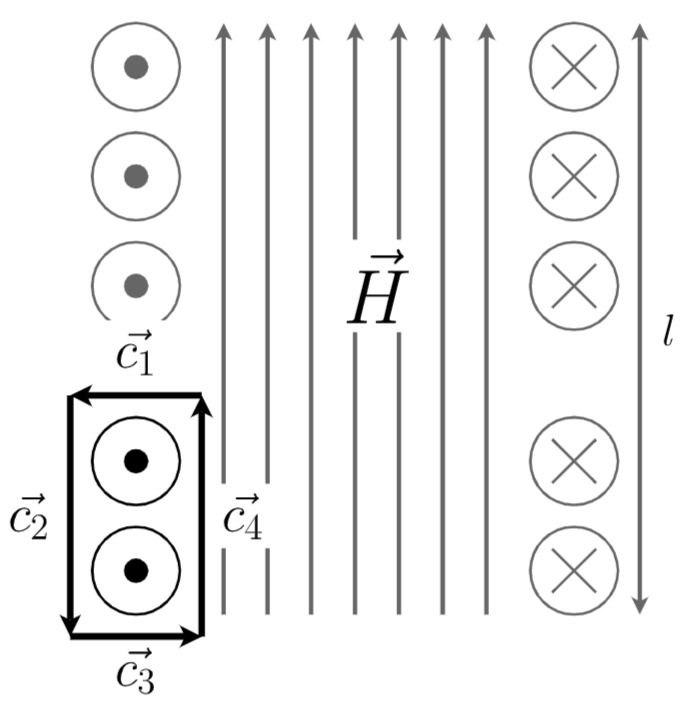
Für den Innenraum ergeben sich somit die Gleichungen:
Berechnung des Feldes der Spulen
Spule 1
Zahlenwerte:
Spule 2
Zahlenwerte:
Betrachtrung der einzelnen Raumgebiete
Im Innern beider Spule überlagern sich die Felder. Es kann die einfache Addition verwendet werden, da beide Felder gleichgerichtet sind.
II:
in diesem Raumgebiet wirkt lediglich das Feld der äußeren Spule, da das Feld der inneren Spule aufgrund der o. a. Näherungen vernachlässigt werden kann.
III:
Aufgrund der o. a. Näherungen verschwindet das Feld in diesem Bereich.
Aufgabenteil b:
Allgemeine Herleitung der Formel zur Berechnung der Selbst- und Gegeninduktivität
Zunächst muss eine Klärung des Begriffs stattfinden: Die Induktivität
Selbstinduktivität
Nun lassen sich die Werte ,rückwärts " berechnen.
Gegeninduktvität
Da sich in diesem Fall die Spule 2 vollständig innerhalb der Spule 1 befindet, ist der Fluss der kleineren Spule vollständig mit dem Fluss der größeren verkoppelt. Es gibt also keinen Fluss, der zwar in Spule 2 ist, aber nicht in Spule
In Zahlenwerten:
Lösung:
Aufgabenteil a:
Für Näherungen siehe Lösungsweg
Aufgabenteil b: