2 / 6

Aufgabenstellung:

Gegeben ist ein magnetischer Kreis mit folgenden Abmessungen: der Eisenquerschnitt beträgt , die relative Permeabilitätszahl wird mit als konstant angenommen. Der linke Schenkel trägt eine Wicklung 1 mit Windungen, der rechte Schenkel eine Wicklung 2 mit Windungen. Der Wicklungssinn ist so gerichtet, dass sich die von beiden Wicklungen erzeugten Flüsse im mittleren Schenkel addieren.

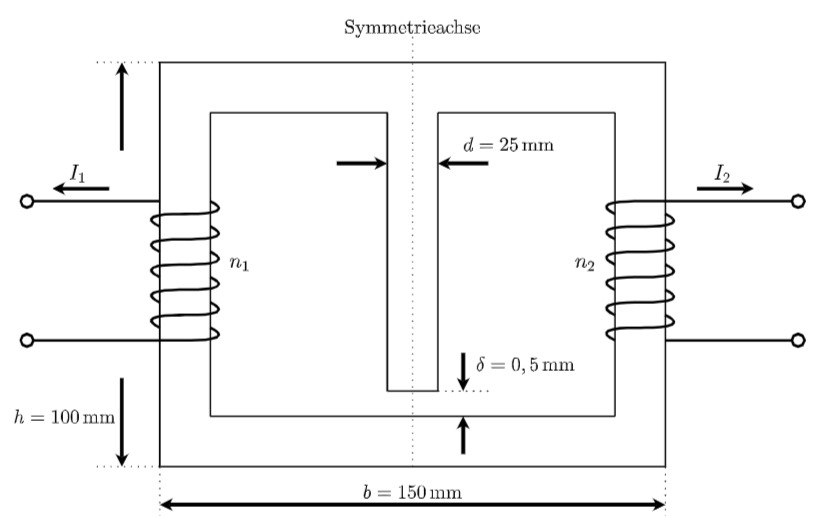
Abbildung

  1. Wie sieht das elektrische Ersatzschaltbild für diesen Transformator aus?
  2. Berechnen Sie die magnetische Feldstärke , die magnetische Flussdichte und den magnetischen Fluss in allen Schenkeln und im Luftspalt für und
  3. Berechnen Sie die Selbst- und Gegeninduktivität sowie die Kopplung

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

 a) Aufstellen des Ersatzschaltbildes

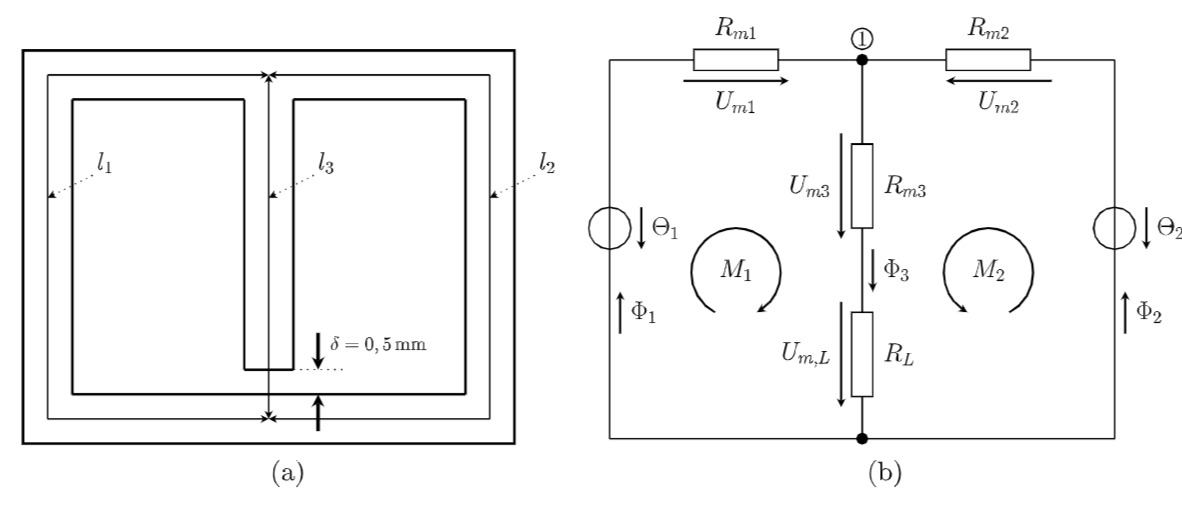
Abbildung

b) Berechnung der Flüsse

Aufstellen der Knoten- und Maschengleichungen:

Nun müssen die einzelnen Variablen der Gleichung berechnet werden. Zunächst die magnetischen Widerstände. Hierzu wird die Gleichung verwendet, wobei die Querschnittsfläche und die effektive Länge beschreibt. Letztere ist die Länge des Weges in der Mitte der Schenkel. Diese Längen bestimmen sich zu:

ü

Hieraus lassen sich die magnetischen Widerstände berechnen. Bei dem Luftspalt ist und kann daher in der Gleichung wegfallen.

Nach der Berechnung der magnetischen Widerstände sind die Durchflutungen zu berechnen. Hierbei bedient man sich der Gleichung

Es ergeben sich daher:

Die nach dem Maschensatz berechneten magnetischen Spannungen können nun gleichgesetzt werden, weil die Durchflutungen gleich groß sind:

Aus der Knotengleichung am Knoten 1 ergibt sich nun

Hiermit lässt sich nun der Gesamtfluss bestimmen. Wir wählen den Umlauf in Masche 1:

Ermittlung der Feldgrößen

da selber Fluss im Eisenkern wie in Luft

c) Berechnung der Induktivität

Berechnung der Selbstinduktivität

Abbildung: Schaltbild zur Berechnung der Selbst- und Gegeninduktivität

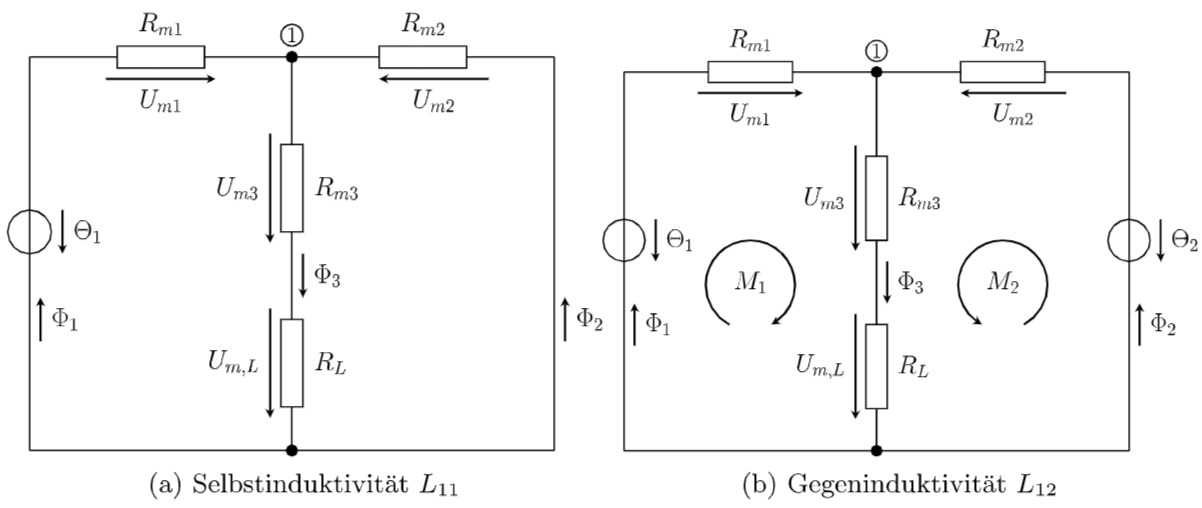
Abbildung

Für die Berechnung der Selbstinduktivität wird die zweite Spule nicht betrachtet und nur der
von der ersten Spule erzeugte Fluss und die daraufhin wirkende Induktivität der ersten Spule berechnet. Es gelten die folgenden Gleichungen:

Hieraus folgen als Zahlenwerte, eine allgemeine Rechnung wäre hier viel zu aufwändig:

Etwas ähnliches gilt für die zweite Spule. Es bleiben gleich: und ändert sich.

Berechnung der Gegeninduktivität

Die Gegeninduktivität beschreibt die Induktivität der Spule , wenn die Spule aktiv ist. Daraus folgt für unser Beispiel: Hier also wobei und ist. Berechnung des Flusses aus über die Stromteilerregel. Der gesuchte Strom verhält sich zum Gesamtstrom wie der der Widerstand, über den der Strom nicht fließt, zum Gesamtwiderstand der Masche. Dies ist möglich, da bereits im vorherigen Aufgabenteil bestimmt worden ist:

Das ergibt für den Gesamtfluss:

Aufgrund der reziproken Materie gilt .
Berechnung der Kopplung

Der negative Koppelungsfaktor drückt aus, dass das Feld der einen Spule das Feld der anderen Spule schwächt.

Lösung:

Aufgabe a: siehe Abbildung Ersatzschaltbild

Aufgabe b:

Aufgabe c: