4 / 5

Aufgabenstellung:

Gegeben sei die Anordnung mit Übertrager und separater Spule. Auf dem linken Ferritkern seien zwei Wicklungen mit den Windungszahlen und aufgebracht. Der Kern habe ein mittlere Kernlänge , die Querschnittsfläche und die endliche Permeabilitätszahl . Der rechte Ferritkern habe dieselbe Querschnittsfäche und einen Luftspalt mit der Länge . Die Permeabilitätszahl des Kernmaterials sei als unendlich angenommen. Vereinfachend kann angenommen werden, dass das magnetische Feld im Luftspalt und in den Kernen homogen sei.

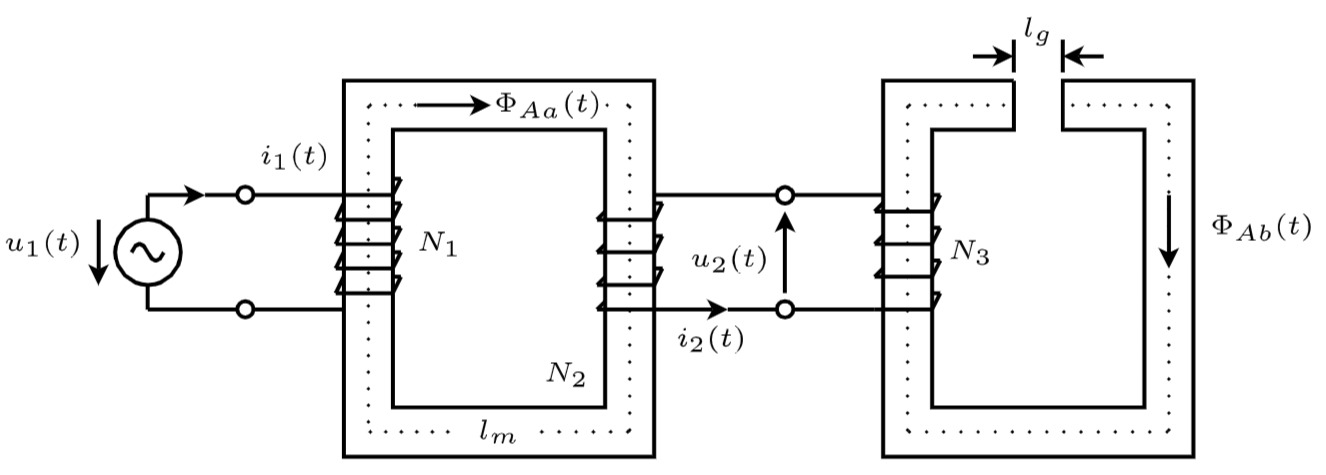
Abbildung

a) Drücken Sie die in der Abbildung eingetragenen Teilfüsse und in Abhängigkeit von den Strömen und aus.
b) Berechnen Sie die Spannung in Abhängigkeit von und , indem Sie das Kurvenintegral der elektrischen Feldstärke entlang der Leiterschleife 1 bilden.
c) Berechnen Sie die Spannung sowohl in Abhängikeit von als auch von . Welcher Zusammenhang besteht damit zwischen den Teilflüssen und Wie hängt die zeitliche Änderung des Stromes von der zeitliche Änderung des Stromes

d) Nutzen Sie die Spannungs-Strom-Beziehung um die an die Spannungsquelle angeschlossene Induktivität der Anordnung zu berechnen.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

Aufgabenteil a)

Wir betrachten zunächst den linken Ferritkern. Das Umlaufintegral der magn. Feldstärke im Kern in Richtung des Flusses liefert dem Durchflutungsgesetz entsprechend den Zusammenhang

Mit der Richtung von orientierten Flussdichte im Kern erhalten wir den Fluss

durch die Querschnittsfläche . Im rechten Ferritkern verschwindet die Feldstärke wegen . Die Integration liefert daher nur im Bereich des Luftspalts einen Beitrag:

Die magnetische Flussdichte besitzt wegen der Stetigkeit der Normalkomponente beim Übergang vom Luftspalt in das Kernmaterial sowohl im Luftspalt als auch im Kern den gleichen Wert Damit gilt für den Fluss im rechten Kern

Aufgabenteil b)

Die Spannung folgt aus dem Kurvenintegral entlang der Schleife :

Aufgabenteil

Kurvenintegrale entlang der Schleifen und :

Aus den beiden Beziehungen folgt unmittelbar der Zusammenhang zwischen den beiden Flüssen:

Einsetzen der Gleichungen ergibt:

und Umsortieren liefert

Aufgabenteil d)

Aus den bisherigen Gleichungen lässt sich die Induktivität bestimmen:

Lösung:

siehe Lösungsweg