Aufgabenstellung:
Ein magnetischer Kreis (siehe Skizze) hat überall den gleichen quadratischen Querschnitt
Für das Blech, aus dem der magnetische Kreis aufgebaut ist, gilt die in der Tabelle gegebene Magnetisierungskennlinie:
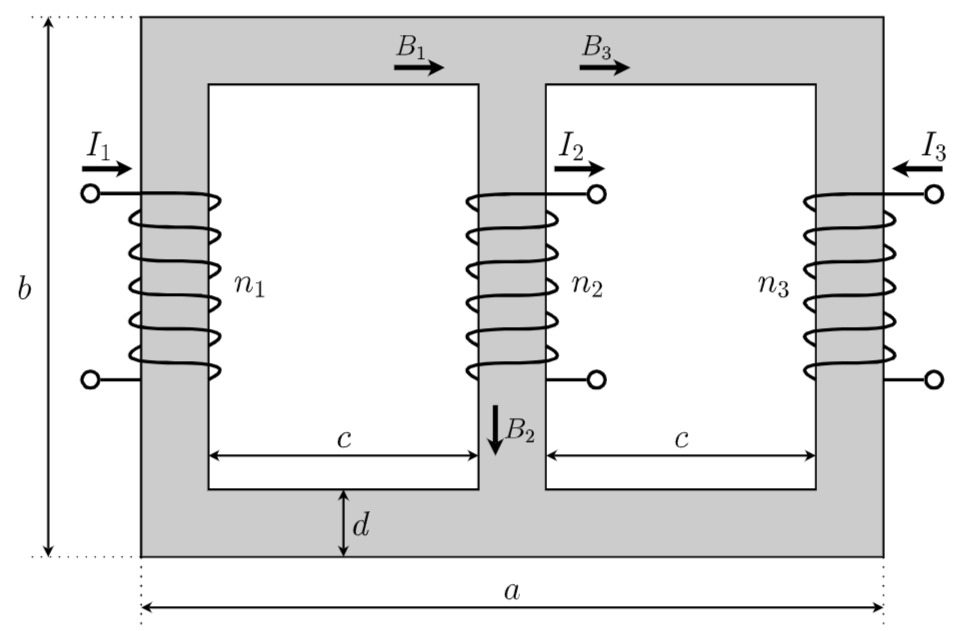
In der rechten Wicklung fließt der Strom
Wie groß muss der Strom
Lösungsweg:
Ansatz
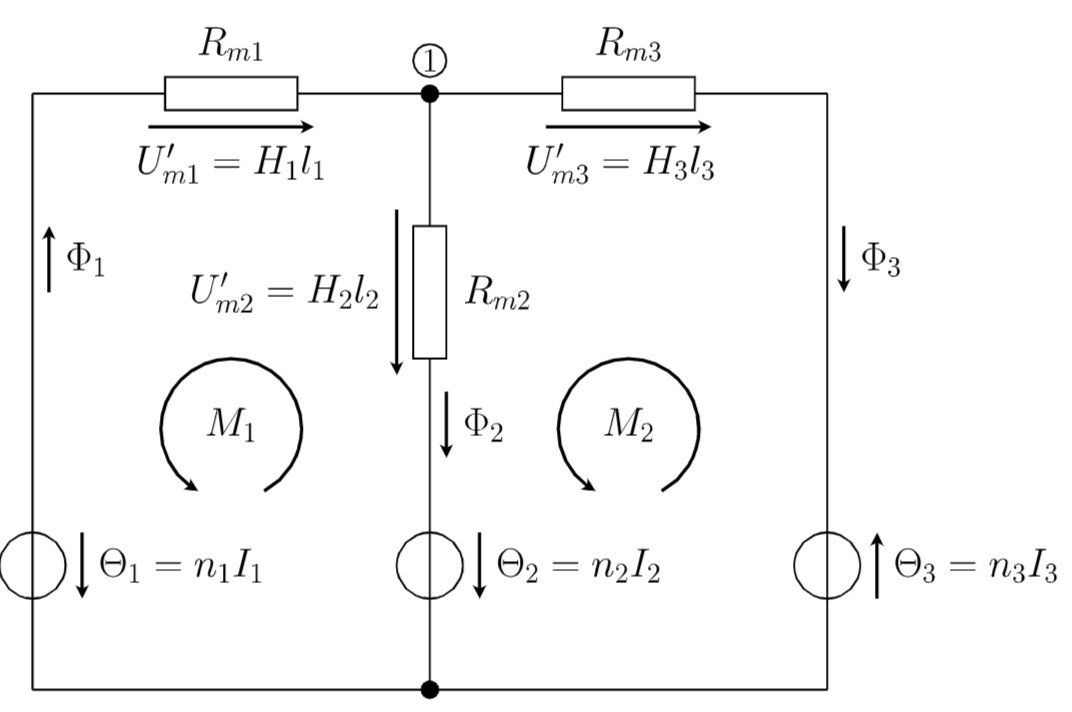
1. Aufstellen eines Ersatzschaltbildes
2. Berechnung der mittleren Feldlinienlänge der Anordnung
3. Berechnung
4. Durchflutungsgesetz in Masche 2
5. Berechnung der resultierenden Flussdichte im Schenkel 1
6. Durchflutungsgesetz in Masche 1
Ersatzschaltbild
Berechnung der mittleren Feldlinienlängen
aus Symmetrie
Berechnung der magn. Feldstärke im dritten Schenkel
Gegeben ist
Anwendung des Durchflutungsgesetzes auf die Masche 2
Das Durchflutungsgesetz
Hieraus ergibt sich aus der Magnetisierungskennlinie eine magn. Flussdichte von
Berechnung der Flussdichte im ersten Schenkel
Die Anwendung der Kirchhoffschen Knotenregel im Knoten 1 ergibt:
Da ein konstanter Querschnitt gegeben ist, lassen sich die Flüsse als Flussdichten schreiben.
Aus der Kennlinie folgt daher eine magnetische Feldstärke von
Anwendung des Durchflutungsgesetzes auf die Masche 1
Lösung:
siehe Lösungsweg