18 / 20

Aufgabenstellung:

AbbildungDer starre Körper   (Masse Massenträgheitsmoment bezüglich Punkt wird im Punkt durch ein Festlager gehalten. Im Punkt ist der starre Körper (Masse Massenträgheitsmoment bezüglich Schwerpunkt ) gelenkig angeschlossen, der im Punkt durch ein Loslager gehalten wird. Im Punkt ist außerdem ein Hubzylinder angeschlossen, der im Punkt durch ein Festlager gehalten wird.

Der Schwerpunkt von Körper befindet sich in der Mitte zwischen den Gelenken und . Alle Gelenke sind reibungsfrei. Der Hubzylinder wird mit der konstanten Geschwindigkeit ausgefahren.

  1. Ermitteln Sie die Koordinate in Abhängigkeit von sowie Sinus und Kosinus des Winkels in Abhängigkeit von
  2. Zeichnen Sie den Momentanpol des Körpers ein und bestimmen Sie seine Koordinaten und in Abhängigkeit von

  3. Ermitteln Sie die Winkelgeschwindigkeiten und der Körper bzw. in Abhängigkeit von und Positive Winkelgeschwindigkeiten sollen entgegen dem Uhrzeigersinn drehen.

  4. Stellen Sie die vier kinetischen Gleichungen auf, die zur Berechnung der Hubzylinderkraft benötigt werden, die im Punkt am Körper angreifen muss.

Gegeben:

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Geometrie

Aus der Zeichnung kann abgelesen werden:

b) Momentanpol

Abbildung

Die Zeichnung zeigt:

c) Winkelgeschwindigkeiten

Körper

Aus folgt:

Körper 2: Drehung um

c) Alternativer Lösungsweg

Körper 2 dreht sich mit der Winkelgeschwindigkeit um :

Im Punkt ist Körper 2 mit Körper 1 verbunden:

d) Kinetik

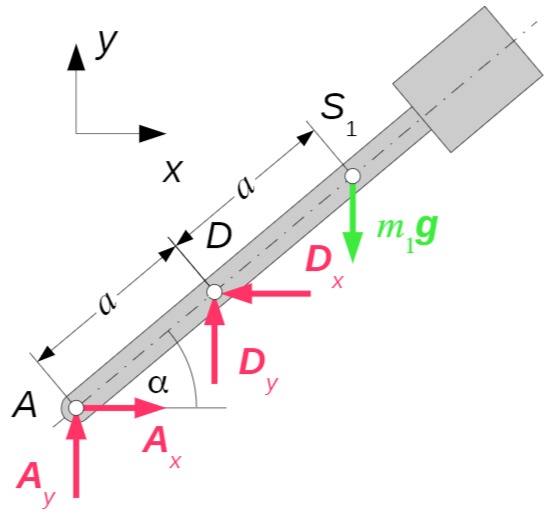
Körper 1 :

Abbildung

Der Schwerpunktsatz liefert zwei weitere Gleichungen, aus denen die Kräfte im Lager ermittelt werden können. Diese sind aber nicht gefragt.

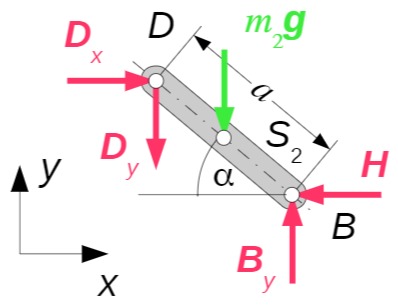
Körper 2:

Abbildung

Lösung:

  1.  
  2.