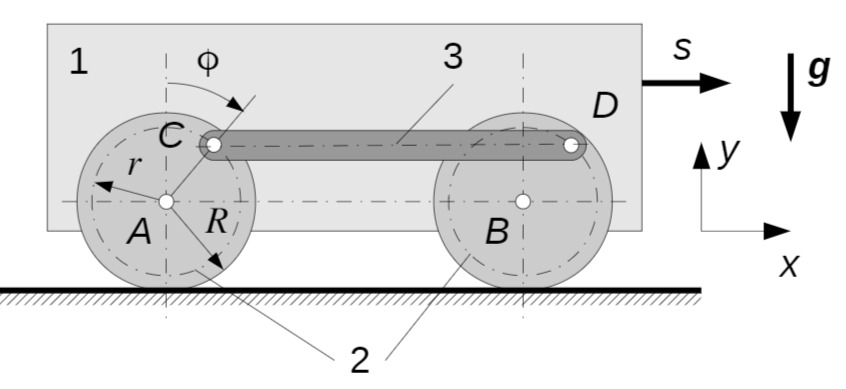Das abgebildete Fahrzeug besteht aus dem Klotz 1 (Masse an den in den Punkten und rechts und links jeweils ein Rad (Masse Massenträgheitsmoment bezüglich Schwerpunkt, Radius reibungsfrei gelenkig angeschlossen ist. An die Räder auf beiden Seiten ist in den Punkten und jeweils eine starre Stange (Masse ) reibungsfrei gelenkig angeschlossen. Die Punkte und haben jeweils den Abstand vom Radmittelpunkt.

Die Position des Fahrzeugs wird durch die Ortskoordinate beschrieben und die Stellung der Räder durch den Winkel . Für gilt und .

1. Ermitteln Sie die Gesamtenergie für eine beliebige Verschiebung in Abhängigkeit von sowie den Komponenten und des Geschwindigkeitsvektors der starren Stangen. Wählen Sie als Bezugsniveau für die Lageenergie den Boden. Setzen Sie die gegebenen Daten ein und fassen Sie zusammen.
2. Ermitteln Sie die kinematischen Beziehungen und
3. Ermitteln Sie die Geschwindigkeit für beliebiges .

Gegeben:

a) Energie