Aufgabenstellung:
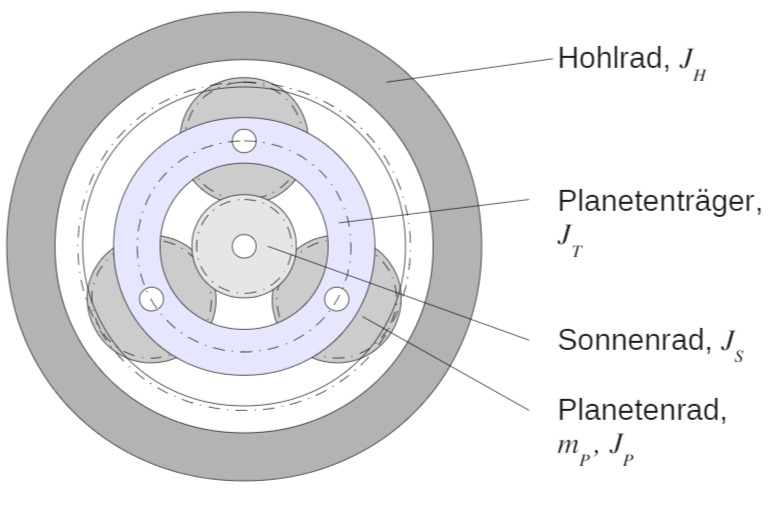 Das abgebildete Planetengetriebe besteht aus dem Hohlrad mit Innenradius
Das abgebildete Planetengetriebe besteht aus dem Hohlrad mit Innenradius
Am Hohlrad greift das Moment
Winkelgeschwindigkeiten und Momente sind positiv im Gegenuhrzeigersinn.
Die Massenträgheitsmomente von Hohlrad, Planetenrad, Planententräger und Sonnenrad werden mit
Wie groß ist die Winkelbeschleunigung
Hinweis: Der Arbeitssatz führt hier nicht zum Ziel. Das Auflösen der mit Schwerpunktsatz und Drallsatz gewonnenen Gleichungen nach der gesuchten Winkelbeschleunigung erfordert etwas Ausdauer.
Lösungsweg:
Kinematische Beziehungen
Die Vorgabe der Winkelgeschwindigkeit
Als kinematischen Größen werden die Winkelgeschwindigkeiten
Geschwindigkeiten am Planetenrad:
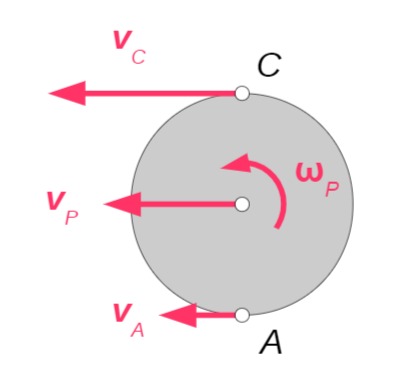
Im Punkt
Im Punkt
Für die Beschleunigungen folgt:
Kinetische Beziehungen:
Sonnenrad
In tangentialer Richtung greifen die Kräfte A der drei Planetenräder an.
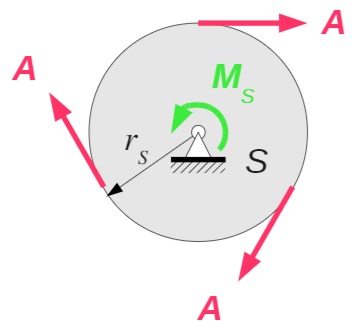
Drallsatz um Punkt S:
Planetenrad
Am Planetenrad greift die Kraft

Schwerpunktsatz:
Drallsatz um Punkt
Planetenträger
In tangentialer Richtung greifen die Kräfte
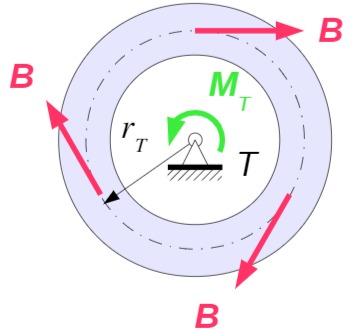
Drallsatz um Punkt
Hohlrad
In tangentialer Richtung greifen die Kräfte
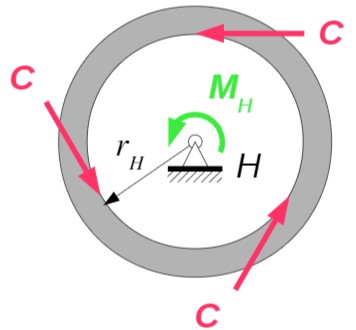
Drallsatz um Punkt
Auflösen der Gleichungen
Mit den vier Drallsätzen
Aus den Drallsätzen für das Sonnenrad, den Planetenträger und das Hohlrad folgt für die Kräfte
Einsetzen von
Einsetzen von
Mit den kinematischen Beziehungen (1) bis (3) folgt:
Die Gleichungen (9) und (10) können z.B. mit der Cramerschen Regel nach der gesuchten Winkelbeschleunigung
Ausrechnen der Determinanten ergibt:
Mit
folgt:
Zusatz: Stationärer Lauf
Im stationären Lauf sind die Winkelbeschleunigungen null, d. h.
Aus den Gleichungen (9) und (10) folgt:
Aus Gleichung (10') folgt
Einsetzen in Gleichung (9') ergibt: