Aufgabenstellung:

Das abgebildete Dreifachpendel besteht aus den Trägern
- Bestimmen Sie die Komponenten
und der Beschleunigungen der Schwerpunkte und der Träger und in Abhängigkeit von den Winkeln. - Stellen Sie alle kinetischen Gleichungen auf, die nötig sind, um die Bewegung des Systems zu berechnen.
- Ermitteln Sie die gekoppelten Differentialgleichungen für die drei Winkel (anspruchsvoll!).
Gegeben:
Lösungsweg:
a) Beschleunigungen der Schwerpunkte
Zuerst werden die Geschwindigkeiten und die Beschleunigungen der Punkte
Träger
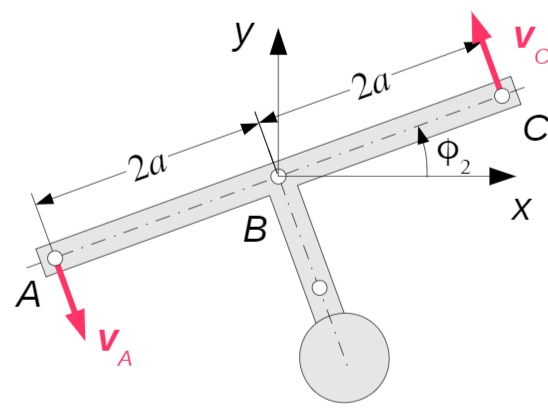
Damit gilt für die Geschwindigkeiten der Punkte
Für die Komponenten der beiden Geschwindigkeitsvektoren folgt:
Ableiten nach der Zeit ergibt die Beschleunigungen:
Als Bezugspunkt für die Kinematik des Trägers
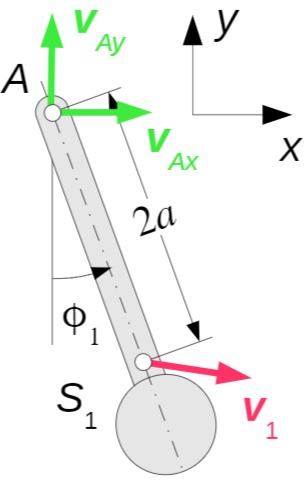
Für die Komponenten des Geschwindigkeitsvektors des Schwerpunkts gilt:
Für die Komponenten des Beschleunigungsvektors folgt:
Einsetzen der Beziehungen für die Beschleunigungen von Punkt
Als Bezugspunkt für die Kinematik des Trägers 3 wird Punkt
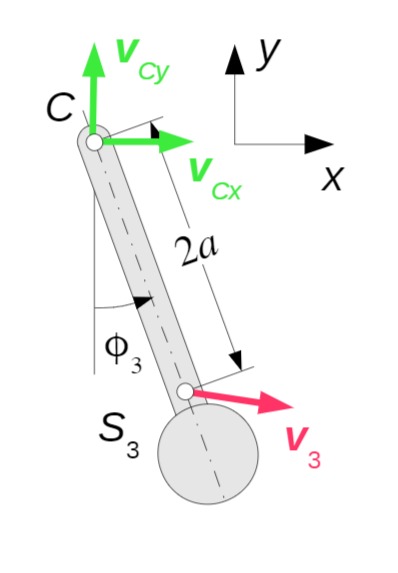
Für die Komponenten des Geschwindigkeitsvektors des Schwerpunkts gilt:
Für die Komponenten des Beschleunigungsvektors folgt:
Einsetzen der Beziehungen für die Beschleunigungen von Punkt C ergibt:
b) Kinetische Gleichungen
Träger 2 dreht sich um den B. Daher wird der Drallsatz Punkt
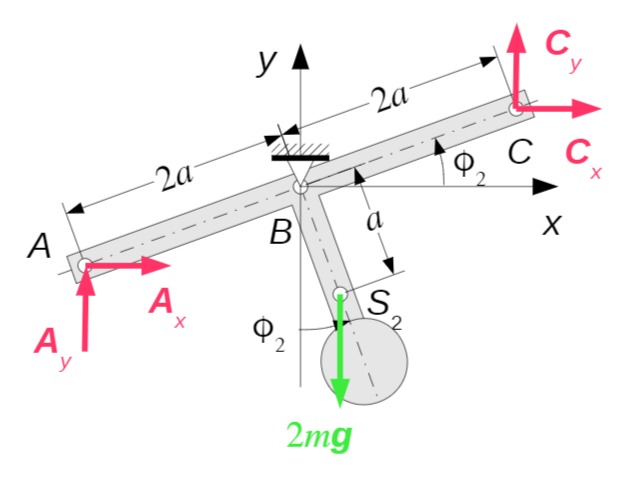
Kürzen durch 2 und Umstellen ergibt:
Für Träger 1 und Träger 3 werden die beiden Schwerpunktsätze und der Drallsatz bezüglich dem Schwerpunkt aufgestellt:
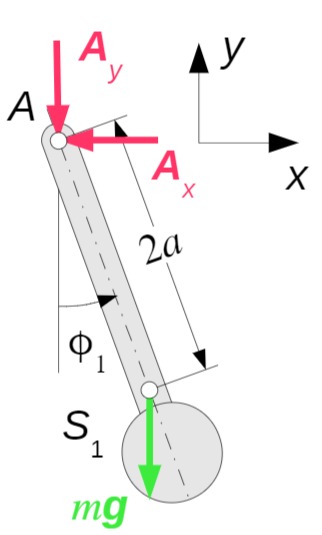
Träger 1
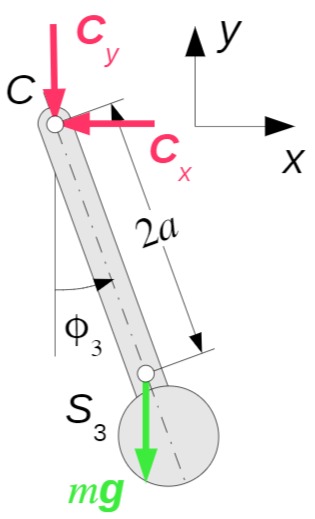
Träger 2
In den Gleichungen (1) bis (11) treten als Unbekannte die vier Komponenten der Beschleunigungen der beiden Schwerpunkte, die vier Komponenten der Kräfte in den Gelenken
c) Gleichungssystem für die Winkel
Zuerst werden die Kräfte aus den Gleichungen (6), (7), (9) und (10) ermittelt:
Als nächstes werden die Kräfte in die Drallsätze (5), (8) und (11) eingesetzt:
Einsetzen der kinematischen Beziehungen
Mit
und
folgt aus Gleichung
Mit
folgt aus Gleichung
Mit
folgt aus Gleichung
Die Gleichungen
Für die numerische Lösung ist es günstig, die Gleichungen in Matrix-Darstellung zu schreiben:
Das System hat acht Gleichgewichtslagen (welche?), in denen die ersten und die zweiten Ableitungen null sind. Von diesen Gleichgewichtslagen ist nur die Lage mit
Lösung:
Siehe Musterlösung.