Kapazität von Kondensatoren

Welche Fläche müssten die Platten eines Kondensators besitzen, der in Luft (Vakuum) bei einem Plattenabstand von die Kapazität aufweisen soll?

Ein Wickelkondensator wird aus zwei einseitig metallisch beschichteten Kunststoffolien gewickelt. Die Kunststoffolie ist dick, die Permittivitätszahl ist 3 und die Durchschlagsfestigkeit Die Fläche jeder Folie beträgt

a) Wie hoch ist die zulässige Spannung?
b) Berechnen Sie die Kapazität des Kondensators.
c) Welche Ladung und welche Energie sind bei im Kondensator gespeichert?
d) Wie gross ist die elektrische Feldstärke in der Folie bei , ausgedrückt in ?

Die planparallelen Platten eines Kondensators mit der Kapazität sind kreisrund, haben einen Radius von und einen Abstand von Berechnen Sie die relative Permittivität des Dielektrikums.

Ein Plattenkondensator mit der Plattenfläche und dem Plattenabstand hat ein Dielektrikum mit der Dielektrizitätszahl . Der Kondensator ist auf die Spannung aufgeladen.

a) Wie groß ist die elektrische Feldstärke zwischen den Platten?
b) Wie groß ist die elektrische Flussdichte zwischen den Platten?
c) Wie groß ist der Betrag der auf jeder Platte vorhandenen Ladung ?
d) Wie groß ist die Kapazität des Kondensators?

In einem Kondensator nach Bild a sind und starke Isolierstoffplatten untergebracht. Ihre Permittivitätszahlen sind und Die Fläche einer Platte beträgt Der Kondensator liegt an der Spannung .

a) Wie groß ist die Kapazität des Kondensators?
b) Mit welchen Spannungen und werden die beiden Isolierstoffplatten beansprucht?

Zwischen zwei konzentrisch angeordneten, dünnwandigen Hohlkugeln aus Metall befinden sich nach Bild a zwei Isolationsschichten mit den Permittivitätszahlen und Die Radien betragen und

Bild: Kondensator mit kugelförmigen Elektroden und geschichtetem Dielektrikum. a) Tatsächliche Anordnung, b) Ersatzschaltung

a) Wie groß ist die Kapazität des Kondensators?
b) Wie groß ist die in der Anordnung maximal auftretende elektrische Feldstärke wenn die zwischen den Kugeln bestehende Spannung beträgt?

Bei einem Koaxialkabel der Länge beträgt nach dem Bild der Radius des Innenleiters und der des Außenleiters Das zwischen beiden Leitem vorhandene Dielektrikum hat eine Permittivitätszahl von .

a) Wie groß ist die zwischen beiden Leitem vorhandene Kapazität

b) Wie groß ist die im Dielektrikum maximal auftretende Feldstärke , wenn die zwischen beiden Leitem wirkende Spannung beträgt? (Bei der Berechnung können Randeinflüsse vemachlässigt werden.)

Bild: Koaxialkabel (Querschnitt)

Ein Koaxialkabel mit der Länge und dem skizzierten Querschnitt ist mit einem Dielektrikum mit der Permittivität gefüllt. Zwischen Innen- und Außenleiter wird die Spannung angelegt.

1. Berechnen Sie die Ladung , die sich auf dem Innenleiter befindet.
2. Berechnen Sie die ortsabhängige elektrische Feldstärke im Dielektrikum.
3. Berechnen Sie die Kapazität des Kabels.

Gegeben ist ein Plattenkondensator mit der Plattenfläche , der durch kurzzeitiges Verbinden mit einer Spannungsquelle auf die Spannung aufgeladen wird, siehe Skizze.

1. Bestimmen Sie die elektrische Feldstärke im Inneren des Plattenkondensators.
2. Bestimmen Sie die Kapazität des Kondensators. Nach dem Trennen von der Spannungsquelle wird der Bereich je zur Hälfte mit zwei Dielektrika aufgefüllt, die die Permittivität bzw. besitzen. Bei wird eine Metallfolie mit vernachlässigbarer Dicke angebracht.
3. Bestimmen Sie die Kapazität des geänderten Kondensators.
4. Welche Spannung stellt sich zwischen den Kondensatorplatten ein?

Die Abbildung zeigt den Querschnitt eines Koaxialkabels mit koaxial geschichteten Dielektrika. Das Kabel hat die Länge . Der Radius des Innenleiters ist , der des Außenleiters . Die Grenzschicht der beiden Dielektrika hat den Radius . Das innere Dielektrikum hat die Permittivität , das äußere entsprechend . An das Kabel wird die Spannung angelegt. Der positive Anschluss befindet sich an der Innenelektrode.

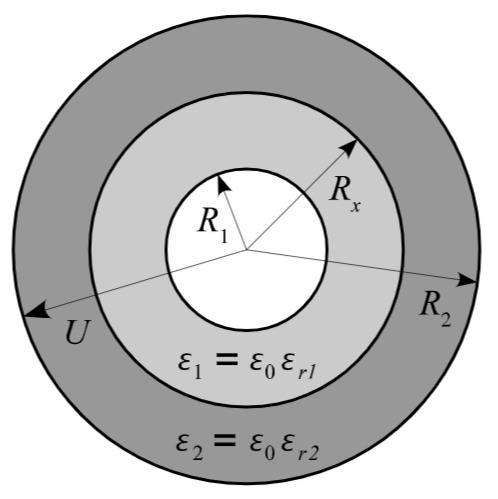
a) Es gelte: . Geben Sie für diesen Fall und als Funktion des Radius an. Skizzieren Sie die Feldlinien der elektrischen Flussdichte und der elektrischen Feldstärke .
b) Berechnen Sie unter der obigen Voraussetzung die Kapazität des Kabels.
c) Es gelte: . Geben Sie für diesen Fall und als Funktion des Radius an. Skizzieren Sie die Feldlinien der elektrischen Flussdichte und der elektrischen Feldstärke .
d) Berechen sie unter der obigen Voraussetzung die Kapazität des Kabels.
e) Es gelte:. .Geben Sie für diesen Fall und als Funktion des Radius an. Skizzieren Sie die Feldlinien der elektrischen Flussdichte und der elektrischen Feldstärke .
f) Berechen sie unter der obigen Voraussetzung die Kapazität des Kabels.

Hinweis:
Die Randeffekte werden als so klein angenommen, dass sie vernachlässigt werden können. Das Skizzieren der Feldstärken (getrennt für - und -Feld) soll das Verhältnis der Felder zueinander in den beiden Raumbereichen widerspiegeln.