Aufgabenstellung:
Im HI-Molekül wirkt entlang der Bindung die Kraft
- Diskutieren Sie die Kraft-Weg-Kurve: Bestimmen Sie Asymptoten, Nullstellen und Extrema.
- Warum ist die Kraft konservativ?
- Diskutieren Sie den Verlauf des Potentials
. Berechnen Sie die TAYLOR-Reihe. - Wie lautet die Kraftkonstante? Mit welcher Frequenz schwingt das Molekül?
Lösungsweg:
Tipp
Kurvendiskussion
Nullstellen: Die Funktion
Maximum/Minimum: Die 1 . Ableitung der Funktion
Asymptoten: Den Grenzwert
Kraftfelder
Vektor = Betrag
Potential eines Kraftfeldes:
TAYLOR-Entwicklung, z. B. harmonische Näherung eines Potentials:
Kraftkonstante:
1. Asymptoten, Nullstellen und Extrema
Skizze: Gezeichnet wird der Betrag der Kraft
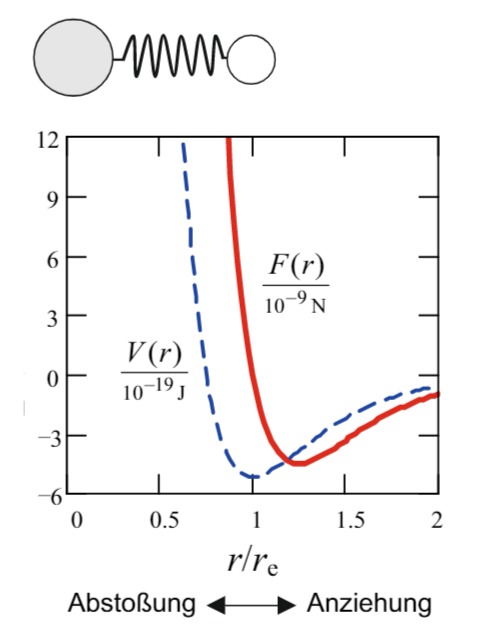
Asymptote:
Nullstellen:
Minimum:
für
2. Begründung: Warum ist die Kraft konservativ
Das Feld ist konservativ (wirbelfrei), wenn rot
Kontrolle: Bilde die partiellen Ableitungen, z. B.
3. Verlauf des Potentials
Durch Integration der Kraft erhält man das Potential (potentielle Energie) der Bindung. Das Energieminimum liegt beim Gleichgewichtsabstand
Die Tiefe des Potentialtopfes heißt Dissoziationsenergie
Potential aufstellen:
Asymptote:
Nullstellen:
bei
Minimum:
Wendepunkt:
bei
Näherung der Potentialfunktion durch eine TAYLOR-Reihe bis zur 2. Ableitung. Die erste Ableitung
Man erhält die harmonische Naherung der Potentialfunktion:
4. Kraftkonstante und Frequenz bei der das Molekül schwinkt
Kraft- oder Federkonstante:
Schwingungsfrequenz:
mit
Es folgt für die gesuchte Frequenz
Lösung:
Siehe Musterlösung.