Aufgabenstellung:
Ein Turmspringer mit einer Masse von
Bestimmen Sie:
-
Die potentielle Energie und die kinetische Energie des Springers direkt vor dem Fall.
-
Die potentielle Energie und die kinetische Energie des Springers bei Auftreffen auf die Wasseroberfläche.
-
Die Energie, die auf das Wasser übertragen wird, wenn das Wasser sich wieder beruhigt hat und der Springer sich wieder an der Wasseroberfläche befindet.
-
Die Masse Wasser, die mit dieser Energiemenge um
erwärmt werden könnte.
Annahme:
-
Die Wasseroberfläche hat die Höhe
.
Hinweis: Die Änderung der inneren Energie des flüssigen Wassers kann mit folgender Formel berechnet werden:
Lösungsweg:
a) potentielle Energie und die kinetische Energie direkt vor dem Fall
Vor dem Fall:
b) potentielle Energie und die kinetische Energie des Springers bei Auftreffen auf die Wasseroberfläche
Die potentielle Energie des Springers beim Auftreffen auf die Wasseroberfläche wird analog berechnet wie die potentielle Energie des Springers vor dem Fall:
Um die kinetische Energie des Springers beim Auftreffen auf die Wasseroberfläche zu bestimmen, wird eine Energiebilanz um den Springer gemacht:
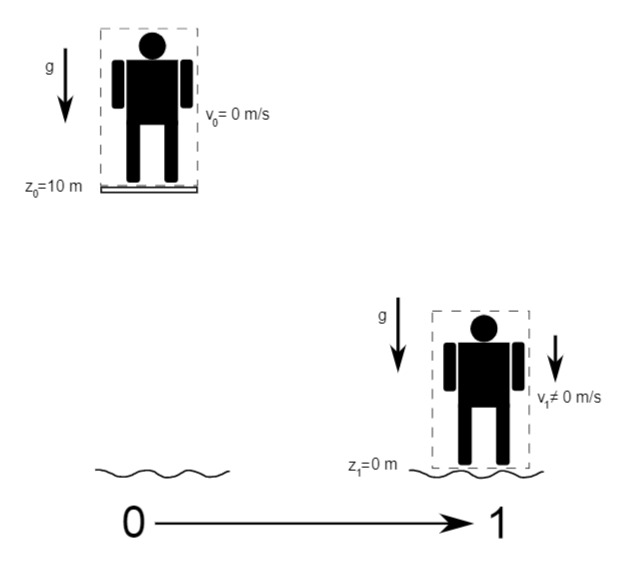
Integrieren führt zu:
Energieerhaltung:
c) Die Energie, die auf das Wasser übertragen wird, wenn das Wasser sich wieder beruhigt hat und der Springer sich wieder an der Wasseroberfläche befindet.
Um die Energie zu bestimmen, die dem Wasser übertragen wurde, wird eine Energiebilanz um Springer und Wasser gemacht:
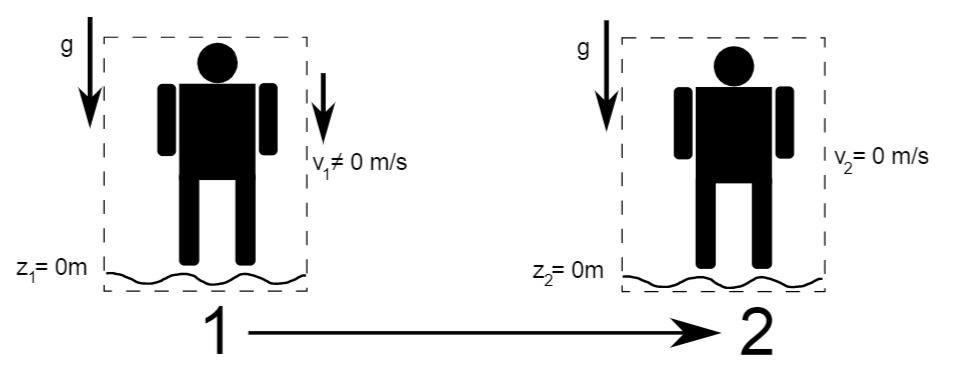
Der Springer hat somit seine gesamte Energie an das Wasser übertragen.
d) Masse Wasser
Die Wassermenge, die mit der zugeführten Energie um
Mit dem Hinweis folgt: