2 / 2

Aufgabenstellung:

Gegeben sei ein Regelsystem mit Strecke , Regler , Führungsgrösse , Stellgrösse und Störgrösse .

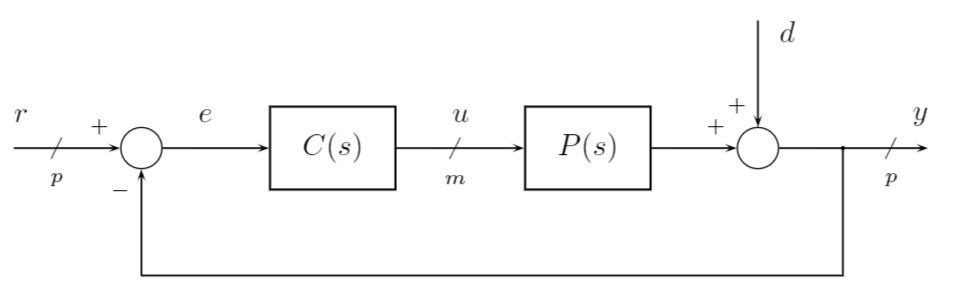
Abbildung

Das Ausgangssignal lässt sich schreiben als

wobei die Übertragungsmatrix der komplementären Empfindlichkeit und die Übertragungsmatrix der Empfindlichkeit bezeichnet.

  1. Leiten Sie die Matrizen der Empfindlichkeit und der komplementären Empfindlichkeit her, indem Sie den Regelkreis einmal bei und und einmal bei und "aufbrechen".
  2. Verifizieren Sie die Identität der Matrizen, , bzw. .
  3. Beweisen Sie den fundamentalen Zusammenhang

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Matrizen der Empfindlichkeit und der komplementären Empfindlichkeit

Um die Übertragungsmatrizen des Regelsystems herzuleiten, bricht man den Regelkreis an einer Stelle auf und schreibt das entsprechende Signal in Funktion der Übertragungsmatrizen der involvierten Systeme und Signale auf. Eine weitere Gleichung wird für das relevante Ausgangssignal aufgestellt.

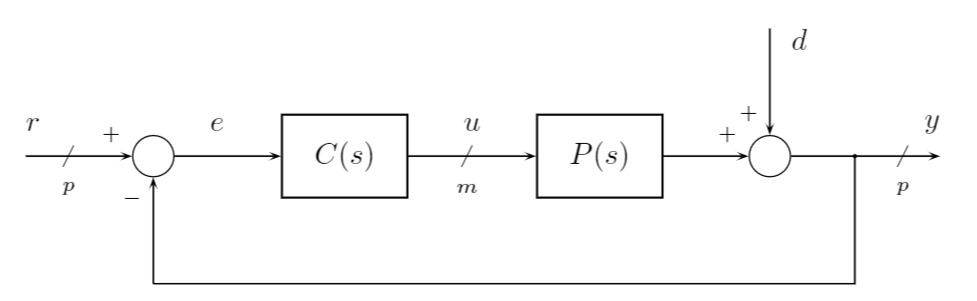
Abbildung

Für den "loop breaking point" bei lauten die entsprechenden Systemgleichungen:

Beachte: Die Matrixmultiplikation ist im allgemeinen nicht kommutativ. Die Reihenfolge der Matrizen muss somit beachtet werden. (z.B: das Signal durchläuft zuerst den Kompensator und dann die Strecke .)

Die Gleichung (1) kann nach aufgelöst werden,

Setzt man diese Gleichung in (Gleichung 2) ein, so folgt:

Damit erhält man für die gesuchten Übertragungsmatrizen der komplementären Sensitivität und der Sensitivität,

Bemerkung: Die Matrix bezeichnet jeweils die Identitätsmatrix mit der entsprechenden Dimension.

Bezogen auf den "loop breaking point" bei lauten die Systemgleichungen

Für die Stellgrösse folgt somit

Eingesetzt in die Gleichung für erhält man,

Für den "loop breaking point" bei resultiert somit die komplementären Sensitivität und die Sensitivität zu

b) Identität der Matrizen, , bzw.

Um die folgenden Matrixgleichungen zu vereinfachen werden sie jeweils von rechts oder von links mit geeigneten Matrizen multipliziert, oder es werden gemeinsame Faktoren ausgeklammert.

c) Zusammenhang

Durch Einsetzen erhält man

Lösung:

  1. , 

    ; 


    ,

  2. siehe Musterlösung 
  3. siehe Musterlösung