Bilanzgleichungen - Zustandsänderungen

1 / 10

Aufgabenstellung:

In einem Behälter mit reibungsfrei verschiebbarem Kolben befinde sich bei einem Druck von bar die Anzahl Moleküle des (idealen) Gases Stickstoff. Die Moleküle besitzen insgesamt eine Innere Energie .

a) Welche Stoffmenge des Gases befindet sich im Behälter und welche Temperatur hat das Gas?

b) Welche mittlere Geschwindigkeit (Wurzel aus dem mittleren Geschwindigkeitsquadrat) hat ein Stickstoff-Molekül?

c) Welches Volumen nimmt das Stickstoff-Gas ein und welche Dichte besitzt es bei diesen Bedingungen?

Das Gas wird nun auf die Temperatur abgekühlt. Bei diesem Prozess nimmt der Druck linear mit dem Volumen ab; dabei verdoppelt sich das Anfangsvolumen.

d) Skizzieren Sie diese Zustandsänderung in einem -Diagramm.

e) Welche Arbeit wird vom Kolben verrichtet und welche Wärme wird umgesetzt? Wird diese Wärme dem Gas zugeführt oder vom Gas abgegeben?

Molmasse .
Ein Stickstoffmolekül soll als starre Hantel behandelt werden,

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

(a) Stoffmenge und Temperatur

Die Stoffmenge ergibt sich aus der Anzahl der Teilchen und der Avogadro Konstante zu

Für ein ideales Gas ist die Innere Energie bei vorgegebener Stoffmenge nur eine Funktion der absoluten Temperatur . Zu berücksichtigen ist die Anzahl der Freiheitsgrade der Moleküle des betrachteten Gases.
Die Innere Energie ergibt sich zu

Jedem Freiheitsgrad wird nach dem Gleichverteilungssatz der Energie die gleiche thermische Energie zugeordnet.
Nimmt man für die zweiatomigen Moleküle des Stickstoffs an, dass im betrachteten Temperaturbereich auch die Freiheitsgrade der Rotation angeregt sind, dann ist die Anzahl der Freiheitsgrade

Man erhält damit für den Anfangszustand ' 1 '

(b) mittlere Geschwindigkeit

Für das Modell des idealen Gases liefert die kinetische Theorie als mittlere kinetische Energie der Translation (Anzahl der Freiheitsgrade )

dabei ist das mittlere Geschwindigkeitsquadrat.

Die Masse eines Einzelmoleküls erhält man entweder aus der Molmasse und der Avogadro Konstante zu

oder alternativ aus der relativen Molekülmasse und der atomaren Masseneinheit zu

Damit ist das mittlere Geschwindigkeitsquadrat für den Zustand ' 1 '

Definitionsgemäß wird damit die mittlere Geschwindigkeit (Wurzel aus dem mittleren Geschwindigkeitsquadrat)

Aus der Zustandsgleichung eines idealen Gases folgt

Die Dichte für den Zustand ' 1 ergibt sich aus der Masse des Gases und dem zugehörigen Volumen mit

erhält man für die Dichte des Gases im Zustand ' 1 '

Lösungsvariante

Die kinetische Gastheorie liefert den Zusammenhang zwischen den makroskopischen Größen der Dichte und des Drucks mit der mikroskopischen Größe der mittleren Geschwindigkeit

Mit den Zustandsgrößen für den Zustand ' 1 ' wird

(d) -Diagramm

Im -Diagramm sieht der beschriebene Prozess folgendermaßen aus (linearer Prozess '1' '2')

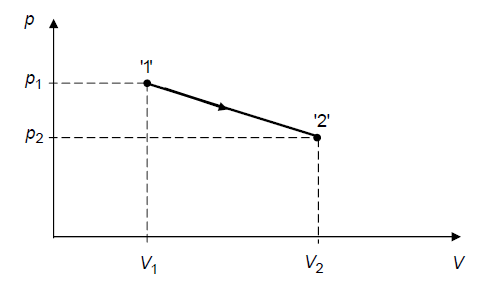
physik

(e) und

Die Zustände ' 1 und '2' sind jeweils gekennzeichnet durch Druck, Temperatur und Volumen.

Anfangszustand ' 1 '

bestimmen

Die Zustandsgleichung eines idealen Gases gilt für den Anfangszustand ' 1 ' und der Endzustand ' 2 ', also

und

oder nach Division der beiden Gleichungen durcheinander

Bei der Expansion ' 1 ' ' 2 ' wird die Arbeit von System nach außen abgegeben; nach der Vorzeichenkonvention gehört zu abgegebener Arbeit ein negatives Vorzeichen. Der Betrag der abgegebenen Arbeit wird im -Diagramm durch die Fläche unter der -Kurve repräsentiert. Zu bestimmen ist also die Fläche des Trapezes.

Die abgegebene Arbeit wird (das Vorzeichen mit einbezogen)

Die Änderung der Inneren Energie hängt nur von der Temperaturdifferenz und ab

Die molare isochore Wärmekapazität bestimmt sich aus den Freiheitsgraden des Stickstoffmoleküls (bestimmt in Teilaufgabe (a)) zu

damit wird

Das Minus-Vorzeichen besagt, dass sich bei diesem Prozess die Innere Energie absenkt.
Der 1. Hauptsatz der Wärmlehre verknüpft die Änderung der Inneren Energie , die umgesetzte Volumenänderungsarbeit und die umgesetzte Wärme

daraus erhält man die beim Prozess ' 1 ' ' 2 ' umgesetzte Wärme

Das Minus-Vorzeichen besagt, dass bei diesem Prozess Wärme vom System abgegeben wird.

Lösung:

;
;
siehe Musterlösung
(Fläche Trapez);